mechanika96

Punki C:

-1-(1 O.l/)² = 5(1 -O.lrf

| ^aCA

³a C 2£_a

= *A ⁴ *CA ⁴ «CA

«A ⁼ «CA. «cW = °CA =    -tf)²

Punkt E:

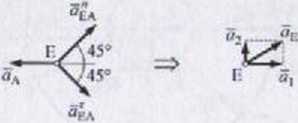
«E ⁼ ^A * ^EA ⁴ ^EA

3c + ^J 0 - ctf

fl, =    • cos 45° + a£_A • cos 45° -a_A -

3-0,1 *-³2(l -0,hf& 0,1 - [0,15 ♦ 7,5(1 -0,lrJ*y5 -0,1

&2 ^{9 a}fU ’^s'ⁿ *5° ^flEA '    *5® =

^<1 - O.lrf 3-0,1

.£

-{b - cif - 3c

.Ł.

2

[7,5(1 -0,1;)? -0,15]-_v'2

- /22 a_E -    ♦ o*

Wyznaczenie przedziałów czasu, w których rzut ^ ma zwrot do góry

^flEA ^{> fl}EA

' -

\b-ct\> ^ 3c^~ =* |b- ct\ > &

-(b-cr f > 3 c

ct\ > y'3c

192

Kinematyka. 2.2.1 Kinematyka tarczy w ruchu pt* »

TT ~~ ^{v r <}    => f > 11,41 s V O < r < 8,59 s

O,1    Oy1

W przedziale 8,59 s < t < 11,41 s wektor ma zwrot w dół. /mianie 2.18

Ifrza prostokątna jest w ruchu płaskim. Wyznaczyć chwilowy środek obrotu Ł pwilową prędkość kątową o> oraz prędkość punktu M metodą chwilowc-środka obrotu.

kierunek v_B

Dane: b

B

kiemnek v,

miwit&wie

^Fu

B|Wiłowy środek obrotu leży na przecięciu promieni r_A, r_B, które są prosto-pllc do prędkości v_A. v_B.

1 • b. r_B - 36, r_M = Jęlbf+b¹ = fib, co ■    ■ ~—

^rA ^b

I * ‘"h ‘ y ³* - ^3,,a

■ ' ^wrM " J ' l/56 * \^^va = 2^4v_a /mimie 2.IM

Ht/a prostokątna jest w ruchu płaskim. Wyznaczyć chwilowy środek pr/y-Jpf- oh D oraz przyspieszenie punktu B metodą chwilowego środka przyspie-/ilustrować położenie D, a_&.

193

'ni.lisku. 2.2.3. Kincnuuyka Uft/y w ruchu phiskun