P1080537

~z~

r/i

1998 r, przyjmując graniczną wartość średniego względnego błędu prognoz wygasłych w/na poziomie 10%.

Rozwiązanie

Wartości prognozowanej zmiennej przedstawiono na rys. 1.14. Analiza wzrokowa wykresu wskazuje, że zużycie energii elektrycznej w firmie „Pako” cechuje się liniową tendencją rozwojową oraz bezwzględnymi wahaniami sezonowymi. Zakładamy, że w okresie objętym prognozą utrzyma się zaobserwowana liniowa tendencja rozwojowa, a wahania sezonowe nie zmienią swej siły Przyjęcie zasady status quo oznacza, że prognosta, przewidując zuzycie energii elektrycznej w firmie „Pako”, przyjął postawę pasywną a wyznaczane prognozy mają charakter krótkookresowy.

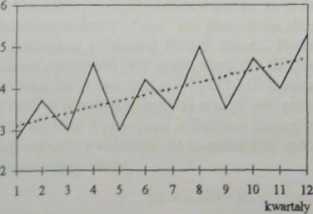
Rys. 1.14 Kwartalne zużycie energii elektryczną w firmie J*ako" w latach 1995-1997

wartości rzeczywiste funkcja liniowa

Do wyznaczenia prognoz skorzystamy z metody wskaźników, budując model addytywny o postaci:

y^y^+c,,

gdzie: yjj - prognoza na okres t w i-tej fazie cyklu,

yjW - prognoza wstępna na okres t w i-tej fazie cyklu,

C| - czysty wskaźnik sezonowości w i-tej fazie cyklu.

Szereg czasowy zmiennej obejmuje 3 pełne cykle, w cyklu występują 4 fazy Prognozę wstępną wyznaczamy przez ekstrapolację linii trendu, Parametry liniowej ftinkcji trendu zostały oszacowane KMNK, a jej postać jest następująca:

y, =2,989+0,147-1 t-1, ..„12.

Algorytm postępowania prowadzący do wyznaczenia czystych wskaźników 'Sezonowości jest podobny jak w przykładzie 1.10 Rozpoczynamy od wyznaczenia wartości zu jako różnic wartości rzeczywistych i wartości teoretycznych, tj. tych, które wynikają z linii trendu I tak dla:

t-1,	1 = 1	Z]j = 2,8- 3,136 = -0,336,
t = 2,	i = 2	Zj.2 =3,7-3,283 = 0.417,
t = 3,	i - 3	= 3 - 3,43 = -0,43,
t-4,	i - 4	z₄₄ = 4,6 - 3,577 = 1,023 itd.

Pozostałe wartości są następujące:

zj.i ** -0,724 Up. - 0,329 z^ = -0,518 z*,₄-0,835,

zj.i- -0,812 zio.2-0,241 *113- -0,606 z₁₂,₄ - 0,547.

W przypadku modelu addytywnego ujemne wartości Zu oznaczają, ze zmienna w i-tej fazie cyklu przyjmuje wartości niższe niz wynikające z linii trendu, a dodatnie wartości zu oznaczają, Ze zmienna w i-tej fazie cyklu przyjmuje wartości wyższe od tych, które wynikają z linii trendu

Wyznaczamy surowe wskaźniki sezonowości jako średnie arytmetyczne

tych wartości zu, które odpowiadają i-tęj fazie cyklu, czyli dla I kwartału z, = I(- 0,336 - 0,724 - 0,812) = -0,624.
dla II kwartału	z, =j(0,417 + 0,329 + 0,241)= 0.329,
dla m kwartału	zj = j(-0,430 - 0,518 - 0,606)= -0,518,
dla IV kwartału	z₄ = -(1,023 + 0,835 + 0,547) = 0,801.

Czyste wskaźniki sezonowości dla każdego kwartału obliczamy, korygując surowe wskaźniki sezonowości wielkością q, wyznaczoną jako średnia arytmetyczna surowych wskaźników sezonowości

q = ^(- 0,624 + 0,329 - 0,518 + 0,80l) = -0,003.

Wyszukiwarka