P1100079
Podtiawiąjąc (1-21) i (1.22) do równania (1.19) i uwzględniając. *a dla reakcji (1.2). kontrolowanej jedynie szybkością transportu substancji. /» ► ri.» ,ub A> > > otrzymuje się równanie kr/ywej pi-ątl-napięcie dla układu odwracalnego. Równunie to jest zgodne z równaniem (4.38).
Joili różnica stężeń nu powierzchni elektrody i w głębi roztworu jest raala, równanie (1.19) można napisać w postaci
(1.23)
■ (!-«) iP
Dla dostatecznie dużych wartości i/4 reakcja olektroclieinlezna biognie tylko w jednym kierunku
gdzie a
|
-Jo cap |
(12*0 | ||
|
/-/* -= |
J9exp |
(-#-) |
(1-25) |
|
wyznaczy |
się < |
otrzymuje się równanie Tafela | |
|
Vm |
=- e±h |
1 Ig |/| |
(1-26) |
|
RT cuF |
In 10 ; |
b-2.ya^ azF |
(1.27) |
|
RT (l-*)zF |
|"A>; |
RT o-^TT^r |
(1.28) |
Dla utleniania anodowego obowiązuje znak plus i równania (1.24). (I -25), a dla redukcji katodowej — znak minus i równania (J.2S), (1-27). Dla małej wartości nadnąp/ęcia aktywacyjnego równanie (1.23) można napisać w postaci (po rozwinięciu w szereg wyrazu eksponcncjalncgo)
(1.29)
zF
RT
Dis układów szybkich natężenie prądu JcsL liniowi) funkcją potencjału.
2. APARATURA DO POMIARÓW ELEKTROCHEMICZNYCH
2.1. WSTĘP
Elementami składowymi zastępczych obwodów elektrycznych, stosowanych dla układów elektrochemicznych, są dwójniki i czwómiki. Idealny opornik, cewka j kondensator stanowią podstawowe dwójniki bierne. Są one charakteryzowane przy pomocy tylko jednego dodatniego parametru. Dla opornika jest to opór omowy Jł (Cl), dh cewki — imSukcyjność własna L i dla kondensatora — pojemność C(F). W ogólnym przypadku dwójnik bierny może stanowić kombinacją wyżej Rn*ymienionych podstawowych elementów, przy czym kombinacją taka może mieć jedynie dwa zaciski (bieguny). Jeśli dwójnik zawiera co najmniej jedno niezależne
energii elektrycznej, nazwany jest dwófilkbm czynnym, Ogólny schemat jajnika przedstawiono ca rys. 2,1, gdzie Z oznacza impedancję Rojnika (opór picW, nktny od częstotliwości prądu), która charakteryzuje zależność pomiędzy
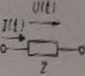
Rys. 2.1. Symbol impcdancji (dwójnik)
mienieni prądu i napięciem. Dla zmiennych prądów i napięć przy zerowych gruntach początkowych zależność pomiędzy prądem i napięciem można wyrazić priMfm Ohma w postaci operatorowej
V i(r)-j$~uw(t) an
gdzie operator p jest zmienną zespoloną
/ = arb (12)
• na sens częstotliwości zespolonej. Wielkość
■ r»-I5T M
obrazuje admitancję dwójnika (przewodność zulcżna od częstotliwości prądu). Przy pisaniu równań często opuszcza się symbol (p).
W elektrotechnice przy obliczaniu obwodów liniowych ze zmiennymi prądami i napięciami stosuje uę dwie metody:
1. Metodę transformacji całkowej Lap!acc’a, która jest odpowiednia dla takich przypadków-kkdy wszystkie napięcia i prądy pojawiają się w momencie r * 0, a przed tym momentem są rótae zeru. Jest ona zatem szczególnie przydatni przy badaniu zjawisk przejściowych.
2. Metodę symbolicznego rachunku zespolonego Steimctza, odpowiednią dla opisu prądów i napięć przy stosowaniu wzbudzania harmonicznego.
Obydwie te metody wymagają wprowadzenia pojęć: impedancja łub adnutancja, które formalnie różnią się tylko operatorem. Dzięki zastosowaniu wyżej wymienionych transformacji lub podstawień liniowe różniczko* o-całkowc równania, które otrzymuje się przy rozwiązywaniu obwodów elektrycznych, redukują się do zwykłych liniowych równań algebraicznych, w wyniku czego rozwiązanie obwodu znacznie się upraszcza.
Uwaga. Zachodzi tu pewne podobieństwo do stosowania logarynnów przy wykonywaniu obliczeń. Każdej liczbie dodatniej jest jednoznacznie podporządkowany jej togaryun dziesiętny, Uóiy jest pewnym obrazem liczby. W związku z tym mnożenie liczb można zastąpić prostszym w wykonaniu dodawaniem logarytmów tych liczb.
Pizy pomocy transformacji Laplace’a funkcji /(/) przyporządkowuje się nową funkcję F(j) zgodnie a równaniem
P(p) - //M«P(-*)dl (14)
które można zapisać w prostszej postaci
F(p)-L[f(t)] CIS)
Funkcja %) jest obrazem funkcji/(r)l jest funkcją zmiennej zespoloną).
31
Wyszukiwarka