P1100106

^Jj,łc jŁM*_t ^pomaian^ w praktyce sajcz^cicj stosuje się «nlwanometr « <j?,._BiłVł oki^cm wsaiuató lub rejestrator o podobnych własnościach, wskazujijoe warloić gsrati

irednic^o /j. dla której obowiązuje rówzioić    ^ ^,au

_ -    *«

^ł> ”* J ?* ^dł    (4-31)

Ciałka występująca no pruwej stronie równania ma znaczenie ładunku przenie-sionego przez prąd chwilowy w czasie trwania kropli- Ł-adunck ten musi być r«5w-ny /_tf Z i — ładunkowi prnsniesionemu przez prąd średni (rys. 4.5).

Rc^r*vnałiie llkoviĆ« dla pr^du średniego ma postać

i# *    - fD¹'****,*'* r_Ł ^ł/* (o — <r₀>    (4.32}

gdzie k «    — 0,627• IO“^J m^a-kg“"^i/3 = 0,627 cm* -g-^.

Średnia wartość prądu dyfuzyjnego nie zmienia się w czasie, co Jest bardzo korzystne z punktu widzenia dokładności pomiaru średniego prądu dyfdzyjRego. I\»nicwaź wszystkie wielkości w>^*^pujące po prawej stronie równania (4.32) &ą stałe d’a danej elektrody i danej substancji elektroaktywnej, rno^na Je połączyć w jedną stałą JE i napisać równanie w postaci

A* — k {c—c₀) == / _t4t—kc₀    (4.33)

gdzie: /_t<ł ==■ A:c — pranicmy prąd dyfuzyjny, ^ = Ar_Ł z i¹

Prąd osiąga graniczną wartość, gdy c_Q *= O. a więc np. dla redukcji przy bardzo Lijernnycłi potoncjałacb (rys. 4.1). Graniczny prąd dyfuzyjny jest wprost prop or-cjonalny do stężenia substancji elektroaktywnej i fakt ter* stanowi podstawę dla wykorzystania go w ilościowej analizie polarograficznej.

\Vlasno4ci prądu dyfazyjnego

Spośród wielkości występujących |>o prawej stronic równania (4.32) jedynie w, i /, zależą od wysokości zbiornika rtęci, zgodnio z równaniami (4.9) i (4.10). Na ich podstawie można wykazać, że średni prąd dyfuzyjny zależy liniowo od pierwiastka kwadnuowego z. wysokości zbiornika. 2^ilcżność ta jest ważnym kry ter i u m odrót* niania prąd u dyfuzyjnego od prądów warunkowanych przez inne procesy niż dyfuzja (na przykład przez reakcję chemiczną).

Przy badaniu zależności średniego prąd u dyfuzyjnego od Lemperntury, trzeba brać pod uwagę przede wszystkim wzajemną zależność Z>, zzt, i r_t. Dla większości jonów    ——    tna wartość 1,63% zza. stopień. Podczas wykonywania oznaczeń

ilościowych trzeba utrzymywać temperaturę na stałym poziomie, co najmniej w granicach    O -S**C. żeby błąd określenia prąd u dyfuzyjnego był mniejszy niż I %.

Ż równania Ilkovi&i widać, że /_rt zależy od <?zz*stb trwania kropli    Zależność

ta przejawia się jedynie przy etuAycfi zmianach /, (wykładni k jest równy I /6). Z równania (4.8) wynika, że c«as trwania kropli j«t wprost proporcjonnluy do y. Z rys. 4.2 widać, ze wartość 7 **!>• w przedziale potencjałów bardziej ujemnych niż potencjał zera elektrokapilamego nzybko maleje ze wzrostem potencjału ujemnego. Odpowia-dające tym zmianom zmiany /j przejawiają się nicznacznyłą spadkiem pnidu dy-fugyincgo przy zmniejszaniu się potencjału ujemnego.

iw

Równamc Ilkovića pomija udział dyfuzji sferycznej w przenoszeniu substancji eJcfctfoaktywncj. Równanie uwzględniające krzywiznę powierzchni kropli rtęci po-chodzi z późniejszego okresu rozwoju polarografii i ma postać

(4.34)

/a ■ ki z F(c-c₀)m, r,(l fk, żj+fc₃ z?)

gdzie

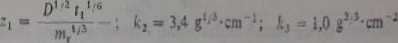
Interesujące jest, że podstawowe równanie Ilkovi£a lepiej odpowiada doświadczalnym wartościom prądu niż dokładniejsze równanie (454), zgodnie z którym wartości powinny być większe, o ok. 10%. Przyczyną tego jest to, k dla najczęściej stosowanej pionowej kapilary nowa kropla wzrasta w kierunku roztworu zawierającego substancję clcktroaktywną o stężeniu zmniejszonym w wyniku elektrolizy przebiegającej na poprzedniej kropli. Jeśli stosuje się mechaniczne zgarnianie kropli lub elektrodę Smolera, w roztworze przy odrywaniu kropli powstają turbulencje wyrównujące stężenia, tak źc wspomniane przenoszenie polaryzacji stężeniowej i jednej kropli na drugą nic występuje. Wyniki pomiarów w tym przypadku są o 10 do 14% wyższe i dobrze odpowiadają równaniu (4.34). Pozorna zgodność doświadczalnych i obliczonych według prostego równania Jlkoyića wartości natężenia średniego prądu dyfuzyjnego bierze się stąd, że wzrost prądu spowodowany dyfuzją sferyczną jest kompensowany zmniejszeniem prądu w wyniku przekazywania polaryzacji stężeniowej.

, Równanie Heyrowsky*ego-Ukovibi i analiza kształtu odwracalnej krzywej polarograficznej

Przyjmuje się założenie, 2e na elektrodzie przebiega redukcja według równania (4.2) i że w roztworze nie występuje postać zredukowana.    *-

Jeśli reakcja elektrochemiczna jest dostatecznie szybka, stężenia postaci zredukowanej i utlenionej (4.2) na powierzchni elektrody (indeks o) określone są potencjałem przyłożonym do elektrody. Stosuje się wówczas równanie Nemsta w postaci

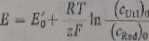
(4.35)

gdzie Łj - potencjał formalny układu (4.2).

Stężenia (f_Ull)₀ i (t'_Red)₀ można w>7naczyć z równań analogicznych do równania (4.33)

(4.36)

(4-37)

U ^m ^ii”ky,|(c_w,)o U ~ k*#d(^Ci«0o

i otrzymane zależności podstawić do równania (4.35). W związku z tym, że w myśl równania (4.33) i dalszego tekstu, zamiast K_nJk_Vll można napisać (Aim/Ajii)^,/j. równanie (4.35) przechodzi w równanie katodowej fali polarograficznej

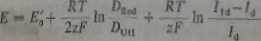
(4-38)

88