P1100115
zakłóca ją pr^adkowy ruch roztworu. Ruch ten wywołuje konwekcyjny transport substancji clektroaklywncj, a co za cym idzie — wzrost prądu. W zwykłych wartuj, ha eh laboratoryjnych równanie (5.2) można stosować jedynie dla pomiarów trwa* jących krócej niż 20-30 s.
Chronoomperometria rzadko jest stosowana do określania stężeń substancji eicktroaktywr.ych. Najczęściej wykorzystywali u jest do wyznaczania współczynników dyfuzji, liczby elektronów biorących udział w reakcjach elektrochemicznych przebiegających na elektrodzie, lub do wyznaczania efektywnej powierzchni elektrod, które w wyniku niejednorodności powierzchni mogą różnić się od powierzchni geometrycznych. W przypadku elektrody nicckranowancj wspomniane wielkości obliczane są z wartości stałej chronoamperometrycznej ekstra polowanoj do punktu /«■ 0.
Chronoainpcrorcetria wykorzystywana jest do określania stężenia w warunkach pomiaru polarograficznego. Szybkość zmiany potencjału jest w tych warunkach lak mała, że potencjał kropli podczas jej czasu trwania zmienia się tylko nieznacznie - jest niemal stały. Przy pomiarach chronoamperometcycznych w tym szczególnym przypadku trzeba brać poprawkę na wzrost powierzchni elektrody, ruch powierzchni elektrody względem roztworu (kontrolowana konwekcja) oraz na sferyczny charakter dyfuzji.
Wszystkie te czynniki uwzględniono przy wyprowadzani u zależności dla prądu (w przypadku równania Ilkosraća uwzględniono tylko dwa pierwsze czynniki). Czfe trw ania kropli jest krótki (3-4 s), w związku z czym grubość warstwy dyfuzyjnej jest niewielka i zakłócenia konwekcyjne nie występują. Prąd jest limitowany wyłącznie dyfuzją i jest ściśle określony. Jak już wspomniano, mierzony jest prąd średni, liniowo zależny od stężenia.
5.2.1. Woltamperoinctria z liniowo zmieniającym się potencjałem elektrody wskaźnikowej
W metodzie tej mierzy się prąd przepływający przez elektrodę, której potencjał zmienia się liniowo w czasie
E — Et—vt
gdzie: v — szybkość zmiany potencjału, Ei — potencjał początkowy.
Potencjał początkowy wybiera się tak, żeby postać układu redoks, która jest obecna w roztworze (na przykład postać utleniona) nie ulegała elektrolizie. W przypadku redukcji
Utl+ze- Red (5.3)
oznacza to, że przy potencjale iT, stężenie postaci utlenionej w każdej odległości od elektrody jest równe stężeniu analitycznemu: cUtlf{x, 0) = c, a stężenie postaci zredukowanej jest równe zeru. Rozwiązanie drugiego prawa Ficka (dyfuzja jest procesem kierującym) dla odpowiednich warunków początkowych i brzegowych prowadzi do skomplikowanych zależności stężenia od potencjału, czasu i odległości
od elektrody. Obliczony na ich podstawie spadek stężenia ( -^,u \
V 9x /»-«
powierzchni elektrody określa natężenie prądu, które wyrażą równanie Rand• lessa-St’v£Jka
/ _p \
I § '*<*'* P^f*) ;t||
gdzie: P “ funkcja szybkości zmiany potencjału i czasu (iloczyn et
podawany jest w jednostkach t - czas liczony od momentu osiągnięcia po-tencjału pólfali) (rys. 5.1).
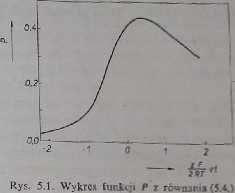
Równanie to obowiązuje dla układów odwracalnych. Prąd jest wówczas wprost proporcjonalny do wartości funkcji P, z czego wynika, że krzywa /-E ma postać piku. Maksymalna wartość funkcji wynosi 0,452 i w związku z tym natężenie prądu dla piku (jest ono zwykle wykorzystywane w pomiarach analitycznych)
,'“0>452Sy^'u>,,,c"''1 (Ł5)
Z równania (5.5) widać, żc J9 jest wprost proporcjonalne do stężenia substancji elektroaktywnej. Zależność ta stanowi podstawę zastosowania omawianej metody w analizie ilościowej. Natężenie prądu jest wprost proporcjonalne do pierwiastka kwadratowego z szybkości zmiany potencjału w czasie.
Z rysunku 5.1 widać, żc maksymalna wartość funkcji P odpowiada wartości argumentu 0,55. Stąd wynika następująca zależność pomiędzy potencjałem piku Ep i potencjałem pólfali układu (temp. 25*C):
E9 = £„,+0,0285/2, V (5.6)
Górny znak obowiązuje w przypadku redukcji, dolny — w przypadku utleniania. Przy potencjale pólfali wartość natężenia prądu stanowi 85,17% wartości natężenia prądu piku. Prąd osiąga wartość 7p/2 przy potencjale £p/2, dla którego, zgodnie z przebiegiem funkcji P, obowiązuje zależność
= £|/2±0,Q280/z , V (5-7)
Potencjał Fp(i można bardzo dokładnie zmierzyć. W przypadku układów odwracalnych potencjał Etn. podobnie jak potencjał Ev, nie zależy od szybkości zmia-
108
Wyszukiwarka