P1100161
Z równania (15.4) wyniku, to jeżeli oświetli się fllir Interfcrcncyjny białym światłem, w Świetle wychodzącym będ/Jc wzmocnione promieniowanie o długościach fal, które równają się całkowitej wielokrotności 2 fln
f kJL »* 2 dn \ (I5.Q
podczas, gdy inne promienie w wyniku interferencji osłabną i wygasną.
Po wielokrotnych odbiciach od lustrzanych płaszczyzn filtra i po wielokrotnej interferencji licznych promieni powstają bardzo wąskie maksima z połówkową szerokością 5-10 nm i r. wartością przepuszczalności w maksimum 30 40%. Można więc uzyskać ze światła białego stosunkowo monochromatyczne promieniowanie. Grubość płytki dobiera się tak, aby była równa i/2 pożądanego promieniowania.
15.3.2. Pryzmaty
Współczynnik załamania wszystkich przezroczystych środowisk zależy od długości fali (dyspersja współczynnika załamania, dn/dA), a więc promieni© świetlne o różnych długościach fali są załamane pod różnymi kątami. Dyspersję wspólczyn-Tiik.i załamaria wyraża w przybliżeniu zależność Cauchy'ego

(13.7)
gdzie o, ó, c — stałe dla danego środowiska.
Z zależności (15.7) wynika, że wartość współczynnika załamania cksponen-©j u lnic maleje z rosnącą długością fali.
Układ dyspersyjny można ogólnie scharakteryzować ^dyspersją kątową (bj, tj. kątem (dó), który tworzą dwa promienie wychodzące z układu, jeżeli różnią się o jednostkę długości fali (ds.)
Przy wyznaczaniu dyspersji kątowej pryzmatu, najczęściej w kształcie równoramiennego trójkąta, wychodzi się z następującego rozumowania:
Równoległa wiązka promieni (rys. 15.5) pada na pryzmat o kącie łamiącym <p
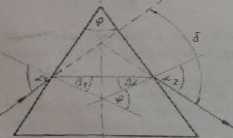
Rys. 15.5. Załamanie światła na pryzmacie
pod kątem padania cc, na pierwszą ścianę Inmiącą pryzmatu. Po przejściu promienia przez pryzmat, jeżeli jest spełniony warunek tzw, minimalnego odchylenia, tj.
je?cli promień przechodzi przez pryzmat symetrycznie, ulcgcić on Łiłatnaniu na drugiej ścirmie pod kątem a?, n zatem jest spełniona zalotność
więc takie pi - 0j ■ P
Promień padający tworzy z promieniem wychodzącym kąt 3, który ma dla rozpatrywanego przypadku najmniejszą wartoió
^ (15.9)
Ponieważ ip « 2/J, współczynnik załamania pryzmatu można wyrazie równością
3+#
cjna sin-s-'
n - ™- - —-—1 (kS.UA
sra# 9
Dyspersję kątową wyraża się w postaci różniczkowej, a ponieważ odchylenie kątowe przy danym kącie podania zależy od współczynnika załamania pryzmatu (ii), o ten z kolei zależy tylko od długość fali (A), można napisać
(15.11)
d$ dn dA ~ dn dA
Po zróżniczkowaniu równania (15.10) i po podstawieniu do równania (15.11) dyspersja kątowa będzie wyrażona wzorem
2 sin
i+9
d n
dA
(15J2)
lab
_dn dT
(15.13)
2 sin &
j/l-t«2sin2|
Z równania (15.13) wynika, że dyspersja kątowa jest wprost proporcjonalna do dyspersji współczynnika załumania i do kąta łumiącego. Dlatego na pryzmaty są wybierane materiały o jak największym współczynniku załamania. Kąt łamiący w większości pryzmatów ma wartość <p = 60°. Dalszo zwiększenie kąta łamiącego mogłoby spowodować całkowite odbicie promieni na ścianach łamiących.
Jedną z wielkości charakteryzujących pryzmat jcswdołnośćj^dzieł^ R. Praktyczna zdolność rozdzielcza wyrażona wielkością bezwymiarową
R -
A
AA
(15-14)
określa zdolność przyrządu spektralnego do rozróżniania długości fali dwóch promieni, które się różnią o bardzo mały przedział AA. Zdolność rozdzielcza większości przyrządów spektralnych waha się w granicach ok. 5000-50000; w przyrządach do analizy izotopowej R osiąga wartość 500 000-600000.
W przyrządach spektralnych najczęściej stosuje się pryzmaty trójkątne z kątem łamiącym ok. 60°. Pryzmat z krystalicznego kwarcu wykazuje dwójłomność. Skle-
193
J* Fltyczne metody
Wyszukiwarka