P1100162

jmjąc dwie symetryczne części — Jedną z prawoeki^tnego. a drugą z Icwoskrętnego kwarcu (pryzmat Corsu. rys. J 5.6.1). można zlikwidować podwojenie linii spektralnych.

Rys. 15.6. ROtfne rodnie pryzmatów; a) Górnu, b) Literowa, c) Rutherforda, d) ‘Amiciego, e) Abbego. f) poleczenie pryzmatu z płaskim zwierciadłem według Wsdswortha. g> pryzmat Fery*ego

A

/<

Stosunkowo często jest używany pryzmat autokolimacyjny z kątem łamiącym 30° — pryzmat Lirtrowa, który ma jedną ścianę funkcyjną lustrzaną (rys. 15.6b). Jak widać na rysunku, działanie takiego pryzmatu jest zgodne z pryzmatem o kącie łamiącym 60°. JcźcJi jest on wykonany z* krystalicznego kwarcu, odpada konieczność stosowania lewoskiątnego i prawoskrętnego kwarcu, ponieważ promienie przechodzą przez pryzmat dwukrotnie, lecz w przeciwnych kierunkach i podwojenie linii jest skompensowane.

W celu zwiększenia dyspersji przez zwiększenie kąta łamiącego są stosowane pryzmaty złożone — pryzmat Rutherforda (rys,. 15.6c), lub pryzmat Amiciego (rys. 15. ód).

Niektóre przyrządy spektralne, np. spektrofotometry, wymagają, aby kąt między wiązką padającą i wychodzącą dla różnych długości fal był stały i aby jednocześnie był spełniony warunek minimalnego odchylenia.

Te warunki spełnia pryzmat Abbcgo (rys. 15.6e). ewentualnie kombinacja pryzmatu ze zwierciadłem Wadswortha (rys. I5.6f)>

Specjalną konstrukcję ma pryzmat Fcryego, który jednocześnie spełnia funkcję układu ogniskującego (rys. 15.6g).

15,3.3. Siatki dyfrakcyjne

Promieniowanie polichrostatyczne można rozłożyć na widmo również za pomocą siatki dyfrakcyjnej. Optyczną siatkę dyfrakcyjną stanowi szereg równoległych szczelin o jednakowej szerokości i jednakowej odległości, wykonanych w postaci dużej liczby rys na przezroczystej płytce, ewentualnie na zwierciadle. Liczba rys

na I ram waha się w granicach 600-1200, a ich całkowita liczba na siatce wynosi 100000 i więcej.

Wiązka promieni równoległych padających na siatkę ulega ugięciu nu rysach. Promienie wychodzące z dwóch rys są spójne i mogą nawzajem interferować. Wskutek interferencji, kiedy za slutką ustawi się soczewkę, w płaszczyźnie jej ogniskowej powstanie szereg maksimów w postaci cienkich linii. Różnice drogi sąsiednich promieni są Całkowitymi wielokrotnościami długości fali; można je określić na przykładzie ugięcia na dwóch szczelinach (rys. 15.7).

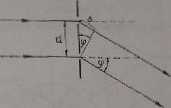
Rys. 15.7. Uglede światła na dwóch szczelinach

d - odległość między szczelinami (stała siatki), A - różnica drogi, ę - kąt ugięcia

Jeżeli linie dyfrakcyjne są odchylone od początkowego kierunku o kąt ip, to różnica drogi

A *= d mp    (15.15)

Jeżeli A ^a k/._t warunek dla maksimum można napisać w .postaci

I dan<p = kX j    (15 .16)

gdzie: d — skala siatki (odległość między rysami); Ar — liczba całkowita, tzw. rząd widmu; X — długość fali.

Z równaniu (15.16) wynika, że maksima dyfrakcyjne poszczególnych długości fal będą się odchylały od początkowego kierunku pod różnymi kątami, co powoduje roztopienie promieniowania polichromatycznego nn widmo.

Z równania (15.16) widać również, że skoro istnieje zależność

pt|

to maksima różnych długości fal obserwuje się pod jednakowymi kątami (rys. 15.8). Na przykład jeżeli )._x ~ 1000 nm w pierwszym rzędzie, pod tyiu samym kątem obserwuje się w widmie również A_a = 500 nm w drugim rzędzie, A₃ « 533,3 nm w trzecim rzędzie i )._A = 250 nm w czwartym rzędzie. Jak więc widać, linie spektralne w poszczególnych rzędach się pokrywają. To pokrywanie można usunąć na przykład przez zastosowanie filtrów przepuszczających tylko pożądany zakres (np. określony rząd widma).

Podobnie, również dla siatek z odbiciem promieni różnicę drogi dla dyfrakcyjnego maksimum można określić na podstawie graficznego obrazu biegu promieni w takiej siatce (rys. 15.9)

(15.18)

A - BĆ-AB =■ t/(sin v>-siny) gdzie: y — kąt padania, <p - kąt ugięcia, d — stała siatki.