P1100198
c
—o
R». 19.20. Dyfrakcju z odbiciem
warunkiem wzmocnienia promieniowania odbitko jcsl to. aby równica drogi dwóch sąsiednich promieni ó = UC \ BU była równa całkowitej wielokrotności długości fali. tj. »ł X,. A*i — dwu sąsiednio szeregi węzłowe
wymieniem warunków dyfrakcji jest równanie Braggów (rys. 19.20)
IM
2d sin 9 «■ n/.
gdzie: d — odległość między płaszczyznami, 0 — Jcąt Braggów, n — rząd dyfrakcji (liczba całkowita)1*. Warunki dyfrakcji promieniowaniu rentgenowskiego na krysztale dokładniej określają tzw. równania lauego:
Jeżeli na kryształ utworzony przez zbiór atomów jednakowo od siebie odległych i leżących na jednej prostej pada promieniowanie elektromagnetyczne (rys. 19.21) pod kątem a*, to rozproszone promieniowanie może się wzmocnić tylko
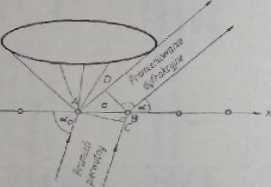
Rys. 19.21. Dyfrakcja promieniowania rentgenowskiego na szeregu węzłowym warunkowi dyfrakcji (wyrażonemu równaniem Lauego) odpowiadają kierunki, które leżą as powierzchni stołka z. kątem wierzchołkowym 180* - 2a
ly Monokryształy niektórych substancji są stosowane do monochromatyzacji ciągłego promieniowania rentgenowskiego albo są analiza torami w spektrometrach (patrs. ryt. 19.7). W takim przypadku d w równaniu (19.21) jest słało. Przy odpowiednio dobranym kącie powstaje dyfrakcja promieniowania o określonej długości fali ż. Z promieniowania ciągłego otrzymuje się więc monochromatyczne promieniowanie rentgenowskie.
Analogicznie, w celu otrzymania widma polichromatycznego promieniowania rentgenowskiego stosuje się monokryształy pewnych substancji. Warunek dyfrakcji (19.21) jest spełniony tylko dla określonego kąta# (przy dowolnej X i stałym d). Zmiana orientacji monokryształu (analiza fora J powoduje zmianą 0 i powstaje dyfrakcja w zależności od A. Każdej długości fali promieniowania rentgenowskiego odpowiada określony kąt 0, pod którym promieniowanie się rejestruje.
wtedy, jeżeli równica drogi promieniowania wtórnego od sąsiednich. wbudowanych cząstek jeal równa całkowitej wielokroteotó długości fali.
Matematycznie
AD-BC — pX
a (cos «—cos «o) *= J*A (19.22*)
Kryształ jest układem trójwymiarowym, równanie (19.22(1) odnosi sie do osi x, analogiczne równania można napisać względem osi y i 2
A (co* P —cos 0o) - «?A (I9.22b)
c (cos y —cos 70) ■ rA (I9.22c)
Równania (19.22* do c) nazywają się równaniami Lauego. Wyrażają one warunki dyfrakcji na krysztale, które muszą być spełnione jednocześnie. W powyższych równaniach symbole a, b, c są to wektory podstawowe, ij. wielkości wektorów trsns-lacyjnych w siatce: aB> Po. Yc słl lo kąty, które tworzy pierwotny strumień, a a, fi, y oznaczają kąty tworzące strumień po dyfrakcji ł osiami krystalograficznymi; p. q. r oznaczają liczby całkowite (równie! 0), które wyrażają różnicę fazową między Talami od dwóch sąsiednich węzłów, a A jest długością fali użytego promieniowania.
Dyfrakcja powstaje tylko na układach okresowych (jakimi są kryształy) i tylko wtedy, gdy A nic zmienia się w czasie, a w przypadku interferencji tylko wtedy, gdy A jest w przybliżeniu równe odległości międzyatomowej, tj. w przybliżeniu 0,1 nrn-Graficznie równania Lnuego przedstawiają stożki pokazane na rys. 19.22
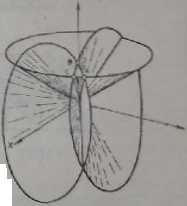
Rys. 19.22. Graficzne przedstawienie równań Lauego równaniu są jednocześnie słuszno (co jest warunkiem powstaniu dyfrakcyjnego promieniowaniu rentgenowskiego), jeżeli punkty A, D, C zejdą się w jednym punkcie
Pomimo uproszczonej postaci praktycznie użyteczne do zrozumienia dyfrakcji jest równanie Braggów i dalej będzie ono stosowane.
19.8.2. Zależność między stałymi sieci i odległością mlędzyp łaszczyznową
Z rysunku 19.20 wynika, źe dyfrakcja powstaje na zbiorze ekwiwalentnych płaszczyzn (str. 263), charakteryzowanych odległością międzypłaszczyznową d i ich orientucją względem osi krystalograficznych.
267
Wyszukiwarka