P1100228

^rfl    '

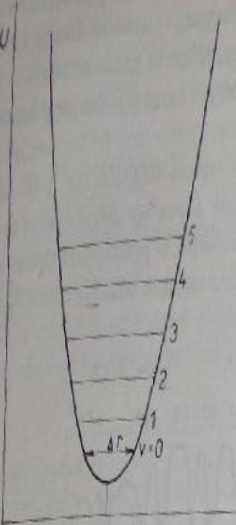
Rys. 22.3, Oscylacyjne poziomy cmm czno cząsteczki dwusłomuwej (o^l¹ harmoniczny)

Częstość ruchu harmonicznego określa wzór

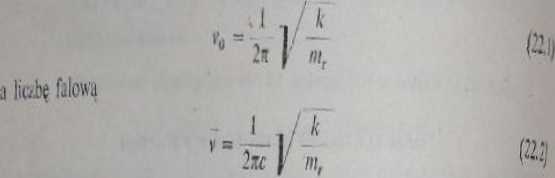
gdzie: v₀ - częstość oscylatora harmonicznego, L - stała siłowa wiązania, | -masa zredukowana atomów (względna), c - prędkość światła.

W, M:

*tf;;    i

gdzie: .V, i Mj - masa molowa atomu 1 i 2, ,\_Ą - stała Avogadra,

Energia oscylacyjna (ruchu drgającego)

fe-■    e, -    m

gdzie: Ej ■ energia oscylacyjna, r₀ - odległość w stanie równowagi, r - odleglck między atomami (większa lub mniejsza od r„).

22.2, WIDMA OSCYLACYJNE

Energia oscylacyjna podobnie jak inne rodzaje energii cząsteczek jest fetowana. Można ją obliczać rozwiązując równanie Scltrddingera dla liniowego oscylatora harmonicznego

E₀*^+yW    .

gdzie: p — oscylacyjna liczba kwantowa, mogąca przyjmować wartości p > 0. 1 2, 3,.... v_Q - częstość podstawowa drgającej cząsteczki.

Cząsteczka znajduje się w stanic podstawowym (E₀)« gdy o » 0.

Po zaabsorbowaniu kwantu energii h* znajduje się ona w pierwszym Mank: oscylacyjnym Ł\ (o = 1). Zgodnie z regułami wyboru dozwolone vą tylko przejścia, które odpowiadają warunkowi Ab — ± 1. Różnica energii między dwoma stanami oscylacyjnymi wynosi

E-E.*

Częstość drgań wiązania jest równa

(22.6)

fi_v - hv

(22.7)

E,»i — E, _ [(^ctl •; t)~(^p + 2)1 ^hv«

un. drgająca cząsteczka absorbuje promieniowanie, którego częstość jest równa częstości drgań własnych wiązania.

Ody cząsteczka absorbuje kwant energii Av\ gd/ic V 2r. to znajdzie się w drugim stanie oscylacyjnym (if₂). Przejścia takie są wzbronione i przejawiają się tylko słabymi pasmami w widmie (wyższe drgania harmoniczne — nadtony). Nadton jest dozwolony tylko w przypadku zakłóceń an harmonicznych oscylatora harmonicznego. Przejścia

E₀±LlE_tJ^h E₂    (22.8)

są dozwolone.

Ponieważ liczba cząsteczek w pierwszym stanic oscylacyjnym zgodnie / prawem Iśoltzmannn jest mała

(22 9)

A^ło

gdzie: A^r,/jV₀ - stosunek liczby cząsteczek w stanie oscylacyjnym E_x i w stanie oscylacyjnym £₀, k — stała Boltzmanna, T - temperatura bezwzględna to i prawdopodobieństwo przejścia £, — E₂ jest małe.

Przejścia E₀ -* E_x są przejściami podstawowymi i w widmie odpowiada im drganie podstawowe. Przejścia E₀ -+ E₂, E₀ -* £T, itd. określa się jako przejścia wyższe, a w widmie odpowiadają im wyższe drgania harmoniczne (nadtony). które są odpowiednimi wielokrotnościami (2 i 3 razy) drgania podstawowego. Różnica między dwoma stanami oscylacyjnymi jest rzędu 0,4 kJ/mol.

Drgania wiązań nie są ściśle harmoniczne tak. że zależność między energią potencjalną a długością wiązania nie jest paraboliczna. Zależność tę przedstawiono na rys. 22.4.

(22.10)

Energię oscylacyjną oscylatora anharmonicmcgo można w przy bliżeniu opisać zależnością

gdzie v — stała unharmonic/ności.