P1100250

24.3-5- Krzywa całkowania

Powierzchnia pod pikiem absorpcyjnym jest wprost proporcjonalna do 5ic*b> jąder, .które absorbują. Przyrządy wyposażone w integrator mogą rejestrować oprći, widma również krzywą całkowania (rys. 24.S krzywa b i rys. 24.7 krzywa c)f Krjty%* całkowania składa się z stopni, których wysokość jest wprost proporcjonalni fc liczby jąder ulegających rezonansowi w danym piku. Takie informacje jakekio*. mnją duże znaczenie dla identyfikacji i analizy strukturalnej. Jeżeli znamy cm;, tyczny wzór związku, lo dzieląc całkowitą wysokość przez liczbę protonów att*_f. nmjcr się przyrost dla jednego protonu. Na tej podstawie można obliczyć ile pr<n> nów chemicznie równoważnych ulega rezonansowi w danym piku. a więc i i te ią, wchodzi w skład grupy funkcyjnej^

24.3.6. Zastosowanie

f Informacjo uzyskane z krzywej całkowania w połączeniu z znajomością mu!i>. pletów. ewentualnie / metodą podwójnego rezonansu, umożliwiają pomyślne r«. wiązywanie zagadnień strukturalnych związków głównie organicznych, ale rów*a i nieorganicznych^ Do celów analizy strukturalnej opracowano systemy i sposoby oznaczania sprzęganych jąder. Nierównoważne protony o małej różnicy przesunie chemicznych oznacza się literami A, B, C itd. Nierównoważne protony o dużej różnicy przesunięć chemicznych oznacza się literami X, A, Z itd. Jako duże pr««ij. nięcic przyjmuje się różnicę chemicznych przesunięć przekraczającą dziesięciokrotną wartość stałej sprzężenia J. Następnie jako przypadek sprzężenia dwóch proton*? rozważa się układy AB, AX i A_x. W przypadku większej liczby nierówiurwałajd protonów sytuacja staje się bard dej złożona. Widma często są zestawiane w ttfó cach z przypuszczalnymi strukturami i porównuje się je z otrzymanym doświadczanie widmem.

Widma MRJ często stosuje się do identyfikacji związków. Z zastosemń ik-ściowych znaczenie ma oznaczanie wody w różnych substancjach. Oznac&M składników mieszanin wykorzystuje różne sposoby wiązania rezor.ujr.cego jjća w oznaczanych składnikach. Szerokopasmowy spektrometr M RJ analizuje caft> wity zbiór rczonujących jąder w różnych zakresach promieniowania radiowcy: Jądrowy rezonans magnetyczny stosuje się również do oznaczania izotopów o jt drowej liczbie spinowej nie równej zeru, występujących obok izotopów tego ttnep pierwiastka* które nie mają spinu jądrowego. Największe zastosowanie tej ir.ctoćj dotyczy badań struktury.;

24.4. ELEKTRONOWY REZONANS PARAMAGNETYCZNY.

ZASADA METODY

Metoda elektronowego rezonansu paramagnetycznego polega na badaniu p-ramagnetyzmu substancji metodą rezonansową. Paramagnetyzm substancji jts konsekwencją spinowego i orbitalnego efektu nicsparowanych ekktronów, bórt występują w wolnych rodnikach, elektronowych stanach trypiętowych i wjowi metali przejściowych.

e

Spinowy I orbitalny efekt powoduje powstanie momentu magnetytznego. Jtadi łubslancję /• nieś parowanymi elektronami umieści się w silnym polu magnetycznym, to wchodzi orientacja elektronowego momentu magnetycznego, podetnie jak dla jądrowego momentu magnetycznego w przypadku MRJ. W podobny *posób pcw-

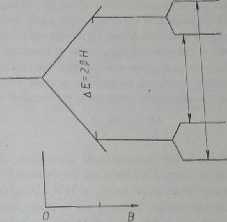
Ryt. 24.8. A — rozszczepienie poziomów energetycznych elektronu w polu magnetycznym, B - dalsze rozszczepienie pod wpływem jadra / — 1/2; przejścia powstałego dubletu zaznaczono

strzałkami

•ł

stają dwa poziomy energetyczne (dla wolnego rodnika) odpowiadające zgodnemu i przeciwnemu położeniu elektronowego momentu magnetycznego wzglądem zewnętrznego pola magnetycznego (rys. 24.8). Powstałe poziomy mają energię określoną przez równanie

£<*    (24.15)

gdzie: B — indukcja pola magnetycznego, m — magnetyczna liczba kwantowa, g - współczynnik Landego.

Wartość tego współczynnika określona jest wzorem

(24.16)

J (J+1)+S(S+1)-Ł(L+1) ¹⁺    2J(J+1)

gdzie: J — całkowita wewnętrzna liczbą kwantowa, S - całkowita spinową liczba kwantowa, L — całkowita poboczna liczba kwantowa.

Wielkość /ia. która występuje we wzorze (24.15) to magneton Bobra (jednostkowy moment magnetyczny wirującego elektronu)

ii

gdzie: e - ładunek elektronu, w. - masa elektronu.

Ponieważ współczynnik Landego dla większości rodników ma wartość równą wartości dla wolnego elektronu, tj. 2,00, a m przyjmuje wartości +1/2 i -1/2, to

371