stat3wzory21

swobody i 2 a)

c) P(t > t_a) = a (tablice: Wartości krytyczne rozkładu t-Studenta o k stopniach swobody i 2cc)

III. X, ~ ?, X₂ ~ ?, «i oraz n₂ duże Statystyka testu:

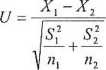
Statystyka Uma rozkład asymptotycznie normalny standaryzowany, przy założeniu prawdziwości hipotezy H₀.

Obszar odrzucenia zależy od postaci hipotezy alternatywnej: .

a)    -P(|£/| > u_a) = a, czyli 0(w_a ) - 1 - y

b)    P(U <u_a) = a, czyli O («_a)= a ,

c)    P(U >u_a) = a, czyli d>(r<_a )-\-a .

Test dla wskaźnika struktury

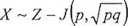
H₀: p= po, p₀ - wartość ustalona

a) Kp.p^po

b) Hi:p<p₀

c) Hi :p> po

duża próba: «>100

Statystyka testu: m

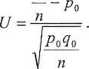
Statystyka U ma rozkład asymptotycznie normalny standaryzowany, przy założeniu prawdziwości hipotezy Ho.

Obszar odrzucenia zależy od postaci hipotezy alternatywnej: .

a)    ,P(|Ł/| > u_a) = a, czyli ⁽b(u_a) = 1 - y

b)    P(U <u_a)~ a , czyli ) = a ,

c)    P(U >u_a) = a, czyli $(«„) = 1 - a .

Test dla dwóch wskaźników struktury

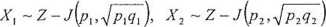
Ho'-P)=p2 a) Kp.p&pz

b) H|: p\<p₂

c) H\\p\>p₂

Statystyka testu:

U = -

,    •    —    ₁    I ¹    "‘2

gdzie q = 1 - p , p = —¹--, n = ——^L—

«, + ?t₂    7i, + n₂

Statystyka U ma rozkład asymptotycznie normalny standaryzowany, przy założeniu prawdziwości hipotezy Ho.

Obszar odrzucenia zależy od postaci hipotezy alternatywnej analogicznie jak dla testu wskaźnika struktury.

Test dla wariancji w populacji

X~N(p,o)

Ho: u² ~a\ ,    cr² - wartość ustalona

Hpcr² > cr₀²

Statystyka testu:

₂ nS²    (77-1)5²

x =—r= i-o-₀ cr₀

Statystyka %² ma rozkład ^² o 77-1 stopniach swobody, przy założeniu prawdziwości hipotezy

Ho.

Obszar odrzucenia:

P(X² >%],)- ^a (tablice wartości krytycznych rozkładu j² o n-\ stopniach swobody)

Test dla dwóch wariancji

X₂~N(jU₂,<T₂)

H₀: cr² = a²

Hper,² >C7₂ Statystyka testu:

^F = % .    gdzie Ś,² > sl

S₂

Statystyka Fma rozkład Fishcra-Snedecora o (?;, - l,7z₂ - 1) stopniach swobody, przy założeniu prawdziwości hipotezy H₀.

Obszar odrzucenia:

P(F>F_a)=a (tablice Fischera-Snedecora ni-l(główka) oraz 112-I (boczek) stopniami swobody)

4