048

Z faktu
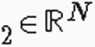
dl Cl IV >2 są liniowo niezależne wynika, że oba wektory:
Wyszukiwarka
Podobne podstrony:
Z faktu dl Cl IV >2 są liniowo niezależne wynika, że oba wektory:
Z faktu dl Cl IV >2 są liniowo niezależne wynika, że oba wektory:
Z faktu dl Cl IV >2 są liniowo niezależne wynika, że oba wektory:
Z faktu dl Cl IV >2 są liniowo niezależne wynika, że oba wektory:
Z faktu ^2 E RN dłaN>2 są liniowo niezależne wynika, że oba wektory: Wybierz co najmniej □ są
Z faktu ^2 E RN dłaN>2 są liniowo niezależne wynika, że oba wektory: Wybierz co najmniej □ są
50 Punkty: 0/1 2 faktu dl(xN>2 wynika, że oba wektory Wybierz co
Z faktu v^2 E J-^2 ^GiV>2 wynika, że oba wektory: Wybierz co najmniej 0 mogą
Z?ktu wynika, ze oba wektroy 2 faktu 1^2 <= J-^2 dlaN>2 wynika, że oba wekto
Z faktu v^2 E J-^2 ^GiV>2 wynika, że oba wektory: Wybierz co najmniej 0 mogą
Z faktu v^2 E J-^2 ^GiV>2 wynika, że oba wektory: Wybierz co najmniej 0 mogą
Z faktu y V ^2 € IRJV,Vl±v2 dlaN>2 wynika, że oba wektory:
Z faktu y V ^2 € IRJV,Vl±v2 dlaN>2 wynika, że oba wektory:
Z faktu y V ^2 € IRJV,Vl±v2 dlaN>2 wynika, że oba wektory:
Z faktu y V ^2 € IRJV,Vl±v2 dlaN>2 wynika, że oba wektory:
Z faktu y V ^2 € IRJV,Vl±v2 dlaN>2 wynika, że oba wektory:
img102 102 8.2. Ogólne własności sieci Hintona Jeśli jednak wektory nie są liniowo niezależne, to wó
więcej podobnych podstron