10

W tej postaci wzór (17) jest zwykle podawany w tablicach do tyczenia krzywych, lecz do obliczeń bez pomocy specjalnych tablic i bez arytmometru można po prostych przekształceniach doprowadzić ten wzór do postaci logarytmicznej:

WS = R tgytg-|.    (17a)

Sposobu powyższego używamy do wyznaczenia punktu S wtedy, gdy kąt (3 jest rozwarty (kąt zwrotu a — mały). Wówczas odcinek WS jest krótki i łatwo go odłożyć. Przy kątach zwrotu a dość dużych możemy korzystać z jednego z dalszych sposobów.

2 i 3. Drugi i trzeci sposób wyznaczenia punktu S polega albo na odmierzeniu odcinka PA na stycznej, albo odcinka na cięciwie i wystawieniu prostopadłych AS lub BS. Trofk^py PAS i PBS są przystające, a więc PA = PB oraz AS = BS, ^Odcięta punktu S, odłożona na stycznej, jest więc równa połowie cięciwy, a rzędna AS — strzałce BS. Długości tych odcinków znajdziemy rozpatrując trójkąt POB:

■    ' =PA =* PB — R sin-~.    (18)

.v>V;    .    •)    \ * ‘

Z wzoru (18) Wynika, że długość całej cięciwy wynosi

£K—2d — S^sin^l*; '    (18a)

s = ĄS~ BŚ ~ OS- OB =* B|l-cósyj.    (19)

Do wzorów (1^ i (19) będziemy jeszcze często powracać, wynika z nich bowiem twierdzenia bardzo ważne w praktyce tyczenia łuków kołowych, odnoszące się nie tylko do punktu S, lecz w ogóle do dowolnego‘punktu M na łuku. Możemy je sformułować w sposób następujący:

W układzie współrzędnych, w którym styczna do koła jest przyjęta jako oś x-ów z początkiem w punkcie styczności, odcięta i rzędna dowołnego punktu M na łuku są odpowiednio równe połowie cięciwy i strzałce łuku o rozpiętości dwa razy większej.

4.    Z punktu P na dwusiecznej kąta WPK lub z punktu K na dwusiecznej kąta WKP odmierzamy cięciwy PS lub KS. Długość tych odcinków znajdziemy z wzoru wynikającego z trójkąta równoramiennego PSO:

PS = KS = 2R sin ~.    (20)

5.    Punkt S możemy również znaleźć wytyczając styczną pomocniczą w tym punkcie (rys. 34 i 35). Punkty Wj i W₂ przecięcia się stycznej pomocniczej ze stycznymi głównymi znajdziemy odkładając na tych ostatnich odcinki PW₁ i KW₂. Nalanie po-łowimy -odcinek W_XW₂ otrzymując punkt S. Wszystki^f(pizpatry-wane tu odcinki są sobie równe i wynoszą

= PWj = W_XS = SW₂ = W₂K = R tg -j. : '    (21)

Na stycznych głównych możemy je odłożyć jednocześnie z odmierzeniem odcinków WP i WK.

Z kolei środek S₁ łuku PS (rys. 35) możemy wyznaczyć, obliczając np. jego odciętą 4 rzędną, z wzorów • ...

PA_X =

= R sin    AiSi = eos .

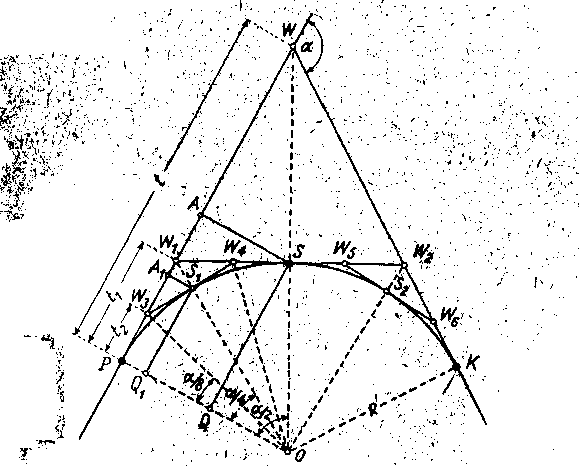
_v •' Rys. 35 ' V

Jak wiemy, otrzymane odcinki są jednocześnie połową cięciwy i strzałką łuku PS. Podobnie odstęp punktu S₁ od wierzchołka W j. określi wzór

Sj = R |sec — 1 j.

' WiSi =

Widzimy, że wzory tych elementów II rzędu mają taką samą postać jak wzory (16)-f-(19), lecz wielkość kąta jest w nich o po-

69