20110111448

4/6

^Andrzej Leśnicki

		( j	(
K(z) = — —+ i— (z-l)' 4 z -1	t Z ~ 4 T z + ~			■

3

Jeszcze przed wykonaniem obliczeń, już wiedzieliśmy, że poprawna może być tylko odpowiedź B. gdyż:

a)    Przyczynowa odpowiedź skokowa musi mieć taką samą wartość pierwszej próbki y[o] jak odpowiedź impulsowa h[o]. Skoro h[0] = 0, to także musi być _y[o] = 0, a ten warunek spełnia wyłącznie odpowiedź B.

b)    Odpowiedź skokowa jest sumą kumulowaną odpowiedzi impulsowej

Suma kumulowana skoku jednostkowego jest funkcją liniową

A-O

^u[k]= u[n\n +1) (analogicznie jak całka funkcji stałej jest funkcją liniową). Suma

A«0

kumulowana sygnału wykładniczego, to wyłącznie w odpowiedzi B.

ISSI

i-<r

m

Taki wynik jest zawarty

Zad. 4. Oblicz i narysuj charakterystyki: amplitudową i fazową, systemu dyskretnego o odpowiedzi impulsowej {//[w]}„.₀ = {l, 1,1,1) korzystając z DTFT, a następnie z 4-punktowej DFT. Wartości charakterystyki amplitudowej dla pulsacji ćo = 0, /r/2; n. - njl to:

A	1,0,0,0
B	a. o.i 2 2
C	4,0,0,0
D	4,2,0,2
Rozwiązanie
H{e^J“)=

1 I 1

■

0    12    3

sin(2o>)

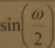
■ jAio

Obliczamy DFT jako próbki widma:

e

11 sin 2*0    .

“F

sin

2