File0033 (2)

q

i

C

co (t u oj

dif

3t

prędkość kętowa)

obwód    cięła-    wahadło

RLC    rok ne    matoma-

aprę -    tyczna

Zynie

Na rysunkc 24.Ib do obwodu RLC dodano nowy element - siłę alekt rornotorycznę e(t). Równania (24.8) przyjmują teraz postać

t

e(t) - L    ■ ~ J l(t) dt ♦ i(t) R (24,13)

. d²q dq ¹

^L *" ⁺ 3t    ^ł r q

dt*

e(t)

(24.14)

-ntZeli napięcie o(t) wytriU3zaj«ce drgania Jest harmoniczne

e( t) = U cos oo t O

(24.15)

wówczas równania (24.14) można zapisać

(j q da i

^L ::s ⁺ st^{R +} e ^q - ^uo ^c°^{9 CJ} *

dt'

(24.16)

1'odobne równanie otrzymalibyśmy rozpatrując np. układ mechaniczny przedstawiony na rys .24 .3.

ozwięzania równania różniczkowego (24.16) poszukujemy w postaci

q( O “ q_Q 8in ( oj t ♦ iy)

gdzie q oznacza amplitudę zmian ładunku. ObliczeJęc

dq( t)

(24.17)

-ar

q o cos ( oj t ♦ q>)

(24.18)

^-'aL|2

dt²

q o sln(oJt+q>)

iC

i podstawiając do równania, po skorzystaniu z tożsamości trygonometrycznych

sin ( u> t +>f) ■ sin (ot) cos ip + cos (co t) sin i?

cos (w t + <p) * cos (ot) cos <p - sin (co t) sinip

Hk&V

otrzymujemy

-|>tn !“<) [^R ¥ ♦ («L - “g) cos^jł    (24.19)

r    i    U ,

cos ( co t) R cos >P - (WL - - —) sinvP — —2_ = o l    ooC    1 uJ

I P(t)“RxCOS^t

m

y

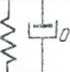
Rys.24.3. Drgający układ mechaniczny wymuszony siłą P(t): k-stała siłowa sprężyny; 0-tłumik drgart (mechaniczny)

Równania (24.19) Jest prawdziwe, niezależnie od czasu t, wta-^dy 9dy obydwa wyrażenia w nawiasach kwadratowych są równocześnie równe zeru, skąd mamy

^w l - -Je ***.....r.....	(24.20)
R^2 * foL - -i-f . -,-L * ' eo C/ _2 2	(24.21)

Obliczając z tego wyrażenia q

61