str030

o6

Zauważmy, że

l = Mflin...nB„) = /_ł(B₁n...nB₍,nfl»₊₁) + _/ł{B_ln...ns_Iln(.Y-B_I,_+l)}.

Stad

m{b, n...nB„n(Y - s_n+1)} =

Niech tfc będzie równe albo 0 albo 1, gdzie ib = 1,2,... , n + 1. Dla dowolnego zbioru B oznaczmy B¹ = B, B° = X — B. Wówczas rozumując analogicznie jak wyżej, otrzymujemy, że

n{B[' n Bj* n... n b*» n b'*₊⁺,') =

A stąd wobec określenia zbiorów £„ otrzymujemy, że lim_n_« p(-En) = 0.

Przypuśćmy, że istnieje x £ X taki, że x 6 lim_n E_n. Wtedy istnieje liczba no £ N taka, że dla dowolnego n > no mamy x £ E„, co jest sprzeczne z określeniem zbiorów £„. Zatem lim_n _.(£n) = 0.

Niech x będzie dowolnym elementem przestrzeni X. Dla dowolnego i £ N, x £ Bi lub x £ X - Bi. Stąd wynika, że istnieje pewien podciąg {nt}).._€H liczb naturalnych taki, że * 6 E_n„ dla dowolnego k £ W. Zatem lim„—« E_n = X.

141. Niech X będzie nieskończonym zbiorem. Rozważmy miarę

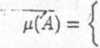
card(A),

co,

gdy .4 jest zbiorem skończonym, gdy .4 jest zbiorem nieskończonym.

Wówczas z^warunku n(A) = 0 wynika, że A = 0.

142.    Przypuśćmy, że /t nie jest miarą czysto atomową. Na podstawie zadania 136, X = Y₀ U U“_v Yj, gdzie n(X₀) > 0. Rozważmy miarę u(E) = ^jr^^(E) dla E £ OT, E C Yo- Oczywiście miara v jest bezatomową miarą i i/(Yo) = 1. Na podstawie zadania 137 istnieje ciąg zbiorów ^-mierzalnych {B„}_n£j| takich, że B_n C Yo, I/(B„) = ^ dla n € W i Yo = U(i,)(⁵i‘ OB,⁵ O...), gdzie {u}t_e« jest dowolnym ciągiem składającym się z zer i jedynek. Stąd wynika, że istnieje zbiór B\' n Bó³ D ... ^ 0, ale ;ł(B‘j^l n Bj³ n ...) = 0. Zatem miara n nie jest ściśle dodatnia.

143.    Wskazówka: skorzystać z zadania 130.

144.    Z założenia lim„_co/r{(A_n — A) U [A — A_n)} = 0. Z równości /t(A) = H(A- A„) + n(Ar\ A_n) dla n £ Ń wynika, że lim_n_oo |i(AnA„) = /ł(A). Z równości p(A„) = p(A„ -4) + /i(.4n4„) wynika, że lim,,-,*/i(A_n) = lim,,-*, p(A O A„). Skąd wynika, że lim«_co p(A„) = n(A).

145.    Niech A będzie takim zbiorem, że miara p rozważana na podzbiorach mierzalnych .4 jest miarą bezatomową. Na podstawie zadania 140 istnieje taki ciąg zbiorów {Brtjaen, że E_n C .4 i lim„__M /»(£„) = 0, lim^,* E_n = 0, linin-o, E_n = .4.

/J

2 założenia ciąg E„ —- E (prawie wszędzie), ponieważ E_n —- 0. Zatem /i(£ A iilRn-eo En) = }i(E A hm„_co En) - 0. Otrzymaliśmy więc, że fi(E) = /r(A-B) -0. Skąd wynika, że ft(A) = 0 i, że /t jest miarą czysto atomową.

146.    Odpowiedź: funkcje stale są jedynymi funkcjami mierzalnymi.

147.    Odpowiedź: funkcje mierzalne maja postać

OO

/ = 2>.U. +ax„.

fsl

gdzie a,-, a £ R, .4; są parami rozłącznymi, przeliczalnymi podzbiorami X, A = A' - (J“! -4(, zaś , Xa oznaczają odpowiednio funkcje charakterystyczne zbiorów Ai oraz A.

148.    Odpowiedź: funkcje mierzalne mają postać

00

f = Yl^aix*i^+a* *•

1    = l

gdzie a,-, a £ R, .4j są parami rozłącznymi, nigdzie gęstymi podzbiorami X, A = X — U”i Ai, zaś \_A , x_A są funkcjami charakterystycznymi odpowiednio zbiorów -4j oraz .4.

149.    Odpowiedź: dowolna funkcja rzeczywista określona^-na X jest funkcją mierzalną.

150.    Wskazówka: skorzystać z równości

X,    gdy c < 0,

^: X*(*) > c} =

A, gdy 0 < c < 1, 0,    gdy c > 1.

151.    Niech / będzie funkcją niemierzalną, na przykład funkcją charakterystyczną zbioru niemierzalnego (patrz zadanie 150). Wówczas funkcja —/ też będzie funkcją niemierzalną, a funkcja / + (—/) = 0 będzie funkcją mierzalną.

152.    Niech A będzie zbiorem niemierzalnym. Rozważmy funkcje niemierzalne X_A, X_x„a- Wówczas \_aXx-a =^> ^a więc będzie funkcją mierzalną.

153.    Niech .4 będzie niemierzalnym podzbiorem X.

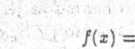
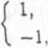
x € A, x £ X - A

•    .U ■    •*■•••• -J •    •

funkcja / jest niemierzalna, a funkcja |/| = 1 jest mierzalna.

154. Niech \_A będzie funkcją charakterystyczną zbioru .4, gdzie /r(A) = 0. Niech / będzie dowolną funkcją. Wtedy

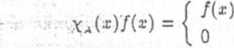
dla x £ A, dla x £ X — A.

Oczywiście funkcja XaS j^est mierzalna. W szczególności ma zawsze żądaną własność.