00312 æ50bbf6d416fbf0edb061aff9ba2fbc

315

Optimizing Defect Levels and Losses from Gage Errors

finaÅ‚ test gage is installed. If the gage error is normally distributed with a standard deviation of 20, then it becomes obvious that several of the reject units will still be sent on to the customer. In addition, several good units will be thrown away as rejects. Utilizing models generated in this paper, it can be shown that the probability of sending a reject on to the customer is 0.01024 and the probability of throwing away a good unit is 0.01624.

A guard band is one means of reducing the defect level of products reaching the customers. Specifically, a guard band is a limit set by the manufacturer on a finaÅ‚ test gage that is tighter than the specification limit established by the customer. The gage loss in terms of good units that are incorrectly rejected should also be determined when adding a guard band. Additional gages will also reduce the defect level to the customer. We will develop models for determining the defect levels and the losses obtained by adding guard bands and additional gages. We will also discuss the complexity of solving these generaÅ‚ mathematical models for optimal operating conditions. A linear model approach is utilized to approximate the morÄ™ complex models, allowing an optimal solution to be generated much morÄ™ easily. An example is provided of this approach.

Basic Models of Defect Levels and Gage Losses

If the product has a distribution f(x) and the gage error follows a distribution g(x), then the probability that a unit xj, that is beyond the upper specification limit, being passed by the gage as a good unit is

(2)

P(good)reject) =    j g(x)dx

FigurÄ™ 1 shows this relationship.

An assumption that will be madÄ™ throughout this research is that the gage errors are normally distributed. With this assumption, an important equality for the risk of having the gage accept the defective unit is

USL

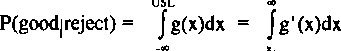
Xj

where g(x) ~ N(xj,ag) and g'(x) ~ N(USL,crg)

(3)