024

Poznamka. Pfiklad lze reśit i ponekud umelym obrałem, uv6donn'me-li si, że 1 + cosa = 2 cos² |a, sina = 2sin |a cos |a.

Dostaneme tak:

z = 1 + cos jTt + i sin = 2 cos² gTt + i • 2 sin g7t cos =

= 2cos (cos gTt + i sin |lt) = \/3 (cos + isin |x)

Ukaźenie si dale reSeni obracene ulohy. Ćislo zapsane v goniome-trickem tvaru yyjadfime ve tvaru algebraickem.

Pfiklad 6

V algebraickem tvaru yyjadfete ćisla

Z\ = 4 (cos |7t + i sin , z-i = § (cos + i sin |n).

Reśeni

Z\ = 4 (cos    + isin |7t) = 4    + i§) = 2\/3 + 2i

z-2 = | (cos    + i sin |rc) = \ (cos §x + i sin §x) = — ^ i

Protoźe jiź umime yyjadrit kornplexni ćislo dane ve tvaru algebraickem tvarem goniometrickym a obracenć, muźeme si na zaver tohoto ćlanku doprat pfiklad jineho typu; pri jeho feseni poużijeme s vyhodou znazornćni komplexnich ćisel v Gaussove rovine.

Pfiklad 7

Z komplexnich ćisel z, pro neż je \z — 25i| ś 15, yyberte ta, ktera maji v intervalu (0,2x) nejmenśi argument.

Reśeni

Komplexni ćisla splńujici podminku

\z — 25i| ^ 15

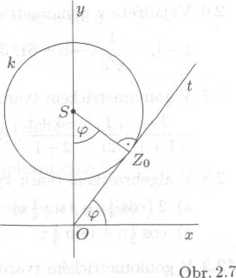
vyplni v Gaussove rovine kruh sc stredem 5, ktery je obrazem ćis-la 25 i, a s polomerem 15 (viz obr. 2.7). Z techto ćisel ma nej-mensi argument p> 6 (0.2n) ćislo zo, kteremu odpovida dotykovy bod Z₀ tećny t vedene z bodu O ke kruźnici k\ je tedy

z₀ = |OZ₀|(cos(p + isinv?),

kde

\OZ₀\ = %/|OS|² - |SZ₀|² =

= \/2ó² - 15² = 20.

Protoże je dale

\OZ₀\    20    4

|SZ₀|    15    3

^COS^ “ |SO| ~ 25 ~ 5 ’    |SO| “ 25 “ 5 ’

dostavame pro hledane ćislo zo s nejmensim argumentem v intervalu

<0, 2tt:)

zo = 20(f + fi) = 12 + 16i.

V§imneme si jeśte, źe mezi komplexnimi ćisly splfiujicimi podminku \z - 25i| < 15 komplexni ćislo s nejmensim argumentem neexistuje. A i kdyż se nas dale nikdo na nic nepta, presto vidime, ktera ćisla z dane mnoziny maji argument ip = ~tz: rnaji jej prave ta ćisla bi, pro nćż je 40 ^ b ^ 10.

47