038

P - 2 ± y/p(8 - 7p) 2(p - 1)

p £ (1, |): dva ruzne realne koreny x_it2 — -^

p = |: dvojnasobny realny koren x\ = x-2 — -3

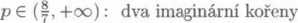
p-2±iy/-p(8-7p)

2(P-1)

Ysimneme si jeste kvadratickeho trojćlenu aa:² + bx -t- c s realnymi koeficienty a, b, c. Tento trojclen lze - jak vite - rozloźit v soućin v pfipade, źe diskriminant rovnice ax² + bx + c = 0 je nezaporny a ćisla x\, X2 jsou jejimi koreny: ax² + bx + c = a(x — x\)(x — a.-₂). Lze tento trojclen rozloźit v soućin i tchdy, je-li diskriminant teto rov-nice zaporny? Ukaźeme, źe ano. Jsou-li totiź X\, X2 koreny rovnice ax'² + bx + c = 0, jejiż diskriminant D je zaporny, plati

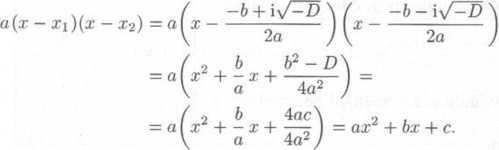
Dostavame tak yysledek:

wWtfil

Każdy kvadraticky trojclen ax² + bx + c s realnymi koeficienty lze vyjadrit. jako soućin a{x - x\){x — x₂). kde a?t, ^x2 jsou koreny rovnice ax² + bx + c = 0.

Rozlożte v soućin linearruch ćinitelu trojclen 4x² — 12x + 25. Reseni

Protoże koreny rovnice 4x² — 122; + 25 = 0 jsou ćisla

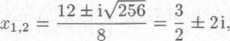
dostavame

4x² - 12x + 25 = 4 (x - § - 2i) (x - § + 2i) = = (2x — 3 — 4i)(2x — 3 + 4i).

Ulohy

3.1 V oboru komploxnich ćisel reśte rovnice:

b) 2x² + x + 1 = 0 d) 3x'² - 7x + 5 = 0

a) x² — 3x + 3 = 0 c) 4x² +3 = 0

3.2 V oboru komplexnich ćisel feSte rovnice: a) (x² + x + l) (x² + x — l) = 0

3.3    Urćete, pro ktere hodnoty realneho parametru p maji rovnice realne, resp. iinaginarni koreny:

a)    px² + 2(p — l)a: +p — 5 = 0

b)    (p + 3)a:² + 3(p - 6)a: + 5 - 18p = 0

c)    x² + 2px + 25 = 0

d)    px² + (2p — l)a: + p = 0

3.4    Rozlożte v soućiny linearnich dvojćlenu trojćlcny:

a) x² + x + 1    b) x² —x + 1

c) 3x² +2x + 2    d) x² — 3x + 5

*3.5 Dokaźte, że i pro imaginarni koreny xj, x₂ kvadraticke rovni-ce x² + px + q = 0 s realnymi koeficienty plati x\ + x₂ = -p, xix₂ — q-

75