1084

= 8 + —= 8,5 (45 -35) + (45 -15)    40

= 8 +

Rozkład częstości pokazuje, źe nie występuje tu zbyt silna asymetria rozkładu (na temat asymetrii rozkładu znajdziemy więcej informacji w rozdziale piątym).

Warunki konieczne do wyznaczenia dominanty są spełnione. Przystępujemy do wyznaczenia dominanty korzystając ze wzoru interpolacyjnego 4.12.

xo = 8; n₀ = 45; n.j =35 ; n+j =15; h₀=2.

(45-35)2

Graficzna metoda wyznaczenia dominanty sprowadza się do wykreślenia histogramu li-czebności trzech przedziałów klasowych, tj. przedziału, w którym znajduje się dominanta oraz przedziałów z nią sąsiadujących. Z góry podstawy najwyższego prostokąta wykreślamy dwie przekątne łączące się z najbliżej położonymi punktami górnych podstaw sąsiednich prostokątów. po czym z punktu przecięcia się przekątnych wykreślamy prostopadłą do osi odciętych. Prostopadła ta wyznacza na osi odciętych wartość dominanty.

Wykres 4.1. Metoda graficzna wyznaczania dominanty

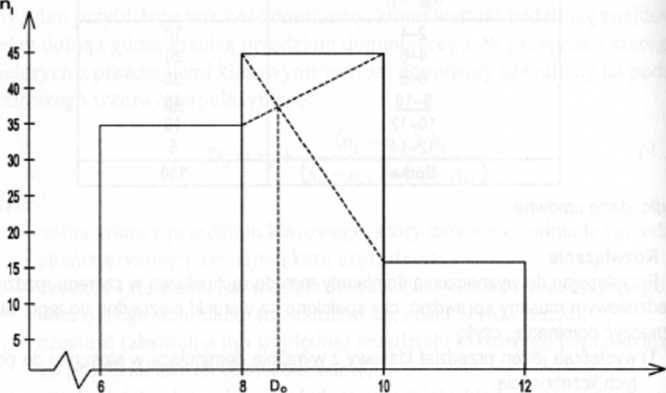
Źródło: opracowanie własne na podstawie tablicy 4.11.

Dominujące wynagrodzenie netto kadry kierowniczej koncernu naftowego wynosi 8.5 ty* siąca złotych.

Dominanta jest pożyteczną miarą położenia w takich dziedzinach jak: badania socjologiczne, badania marketingowe.badaniarynkuitd.Nicpodlcgaona wpływowi war* tości skrajnych. Możnająstosować zarówno w przypadku analizy cech mierzalnych, jak i niemierzalnych.

Przy interpretacji modalnej należy pamiętać, że charakteryzuje ona jednostki statystyczne o typowym poziomie badanej zmiennej, nie zaś wszystkie badane.

Dominanty nie wyznaczamy w szeregu, w którym występuje kilka wartości cechy z podobną częstością, np. nic wskażemy modalnej w następującym szeregu: 2, 2, 5, 5, 6, 8, 8, 10, 10. Żadna z wartości cechy nie przyjęła tutaj pozycji dominującej (cztery wartości cechy powtarzały się dwukrotnie). Mówi się czasami w takiej sytuacji, że dominanta jest wielokrotna.

Zdarza się, że dominanta nie istnieje, zachodzi to wtedy, kiedy żadna z wartości cechy nie powtarza się.

Wyznaczenie dominanty w arkuszu kalkulacyjnym Exccl wygląda analogicznie, jak średniej arytmetycznej. Aby wyznaczyć dominantę wybieramy funkcję Wyst.Najczęściej. Exccl nic obliczy dominanty, jeżeli wszystkie warianty cechy są różne.

Mediana i pozostałe kwantyle

Mediana jest to wartość, która jest umieszczona dokładnie w środku, pod warunkiem, że mamy do czynienia z uporządkowaną (z punktu widzenia badanej cechy) zbiorowością według wielkości jej elementów, tzn. od ich wartości najmniejszej do największej.

Mediana dzieli zbiorowość na dwie rówme części w ten sposób, że połowa jednostek zbiorow-ości ma wartości cechy niższe lub równe medianie, a połow^ra ma wartości cechy rówme lub większe od Mc.

50%    50%

Mediana zwykle jest oznaczana przez Me lub za pomocą litery x ze znakiem ~ u góry x.

Posługiwanie się medianą w życiu codziennym może się okazać bardzo wygodne i czasooszczędnc. Na przykład, aby sprawdzić, jaki jest przeciętny w^rzrost dzieci w- przedszkolu nie jest konieczne mierzenie wszystkich, jak to ma miejsce przy obliczaniu średniej arytmetycznej. Do wyznaczenia mediany wystarczy ustawić dzieci w szeregu według wzrostu i zmierzyć wyłącznie wzrost dziecka znajdującego się w środku szeregu (jeżeli liczba dzieci jest nieparzysta) lub dwójki dzieci znajdujących się w środku szeregu i wyznaczyć medianę jako średnią arytmetyczną ich wzrostów (jeżeli liczba dzieci jest parzysta).

Sposób wyznaczania mediany zależy od rodzaju szeregu statystycznego, z którym mamy do czynienia (formy prezentacji materiału statystycznego).

Jeżeli informacje o wartości cechy przedstawione są w postaci szeregu szczegółowego (nicpogrupowane), to w celu wyznaczenia mediany należy uporządkować informacje rosnąco i ustalić, która z nich zajmuje miejsce środkow^re. Wartość tej cechy będzie wartością mediany. W tym przypadku sposób wyznaczenia media-

107