1087

x₀ = 6; h₀ = 2; n_a = 37; Nr_Me = 66; /u / = 20.

Me = *„ + ^ (M- - _n )= 6 + ^ (66 - 30)= 7,95 = 8 n₀    37

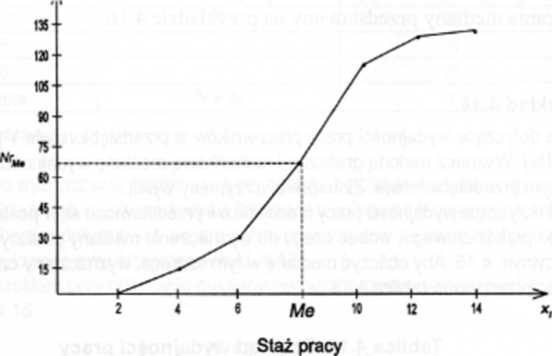
Graficzny sposób wyznaczenia mediany w tym przykładzie przedstawia wykres 4.2. Wykres 4.2. Metoda graficzna wyznaczania mediany

£5

o.

1

Źródło: opracowanie własne.

Mediana stażu pracy w tym przedsiębiorstwie wynosi 8, co oznacza, że połowa pracowników tego przedsiębiorstwa ma wydajność pracy wynoszącą 8 sztJgodz. lub mniej, a druga połowa ma wydajność pracy wynoszącą 8 szt./godz. lub więcej.

Mediana jest bardzo wartościowym miernikiem analizy statystycznej, dzięki swoim własnościom:

•    może być ona wyznaczana w szeregach o otwartych przedziałach klasowych,

•    można ją wyznaczać do opisania zbiorowości, których nic można określić liczbowo (do wyznaczenia mediany nie jest konieczna znajomość wszystkich wartości cechy mierzalnej),

•    jest jedyną średnią, którą można w^fyznaczyć dla rozkładów' skrajnie asymetrycznych,

•    nie jest wrażliwa na wartości skrajne (w przeciwieństwie do średniej arytmetycznej),

•    może być wyznaczana w^r szeregach o nierównych rozpiętościach przedziałów klasowych, tj. w sytuacji, kiedy niemożliwe jest wyznaczenie dominanty.

Wyznaczenie mediany w arkuszu kalkulacyjnym Exccl wygląda analogicznie, jak średniej arytmetycznej. Aby wyznaczyć medianę wybieramy funkcję Mediana.

Jeżeli konieczna jest bardziej szczegółowa analiza właściwości strukturalnych, oprócz mediany, która jest kwartylem drugim, znajdują zastosowanie kwartyl pierwszy i trzeci. Kwartyle należą do miar statystycznych zwanych kwantylami, które dzielą zbiorowość statystyczną w określonej proporcji.

Kwantyle

Kwartyle    Decyle    Centyle

(percentyle)

Kwartyle Q dzielą populację z dokładnością do ćwiartek, decyle D dzielą populację z dokładnością do dziesiątek, centyle C dzielą populację z dokładnością do pojedynczych procentów.

Kwartyl pierwszy (?, dzieli zbiorowość na dwie części w ten sposób, że 25% (1/4) jednostek zbiorowości ma wartości cechy niższe bądź równe wartości Q_{, a 75% (3/4) równe lub wyższe od wartości tego kwartyla:

25%    75%

Kwartyl trzeci Q₃ dzieli zbiorowość na dwie części w ten sposób, że 75% (3/4) jednostek zbiorowości ma wartości cechy niższe bądź równe wartości Q_y a 25% (1/4) równe lub wyższe od w'artości tego kwartyla:

^xmin    Q₃    X_ma

75%    25%

Kwartyle wyznacza się w sposób analogiczny do obliczania mediany, z tym że należy uwzględnić konkretny numer kwantyla.

W przypadku danych uporządkowanych rosnąco i przedstawionych w postaci szeregu szczegółowego wartości kwartyla pierwszego i trzeciego możemy wyznaczyć poprzez podzielenie zbiorowości na dwie części: pierwszą, której jednostki przyjmują wartości nic większe od mediany i drugą złożoną z pozostałych jednostek. Dla każdej z tych części należy obliczyć ponownie medianę korzystając ze wzorów 4.13 lub 4.14. Wartość mediany z pierwszej części będzie odpowiadała kwartylowi pierwszemu Q_haz drugiej części kwartylowi trzeciemu Q_y

Może się zdarzyć, że numer kwartyla nic będzie liczbą całkowitą. Wówczas bierzemy pod uwagę średnią arytmetyczną z wartości cech znajdujących się na miejscu poprzedzającym i następującym po numerze kwartyla.

113