50
92 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków
Funkcja Lagrange’a dla mechanicznej części wibratora ma posiać: L-^mx2 + sindj)~ + ira2(x + e$2sinf>2)“ + “^1$? +”^2^2 +
-—kx2 - mgx - mlg(x - <2 cos ) - m2g{x - e cos $2) gdzie e jest promieniem niewyważenia, jak to pokazano na rysunku 47.
Wykonując zaznaczone działania oraz uwzględniając, że ml=m2=me oraz J{= J2- Js, możemy napisać:
L - i (m + 2m)x2 + mee{\d, sin + $2 sin $2 )i + i me<22 (df sin2 + £2 sin2 $2 ) +
+ d-d2)--^-/^2 - {m + 2me)gx + mege(cost{ + cos£2) (11.2)
Ponieważ współrzędne układu, za pomocą których zapisana jest funkcja Lagrange’a są od siebie liniowo niezależne, możemy napisać równania dynamiki mechanicznej części wibratora, wykorzystując równania Lagrange’a drugiego rodzaju:
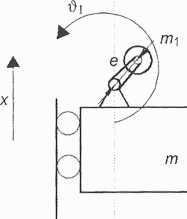
Rys. 47. Rysunek przedstawiający poglądowo mimośród e
(11..la)
(11.Ib)
— [(m + 2me )x + mee{p{ sin d, + ó2 sin t!>2 )]+ kx + (m + 2me )g = -Dxx dt
J — + mee—(i: sin ) + mee2 — fe, sin2 ilj) - cos +
dt' dt dt
- —m e2óf sin(2^1)+megesin^1 =TeII -Dei}}
(U. 3c)
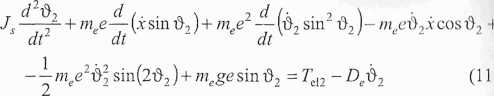
Po wykonaniu zaznaczonych działań w równaniach (10.3) i uporządkowaniu zapisu otrzymamy:
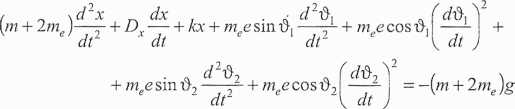
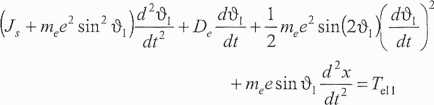
+ mege sindj +
(11.4a)
(11.4b)
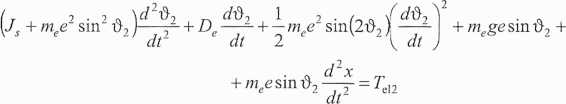
(11.4c)
Układ równań różniczkowych (11.4) jest układem nieliniowym i jako taki nic ma rozwiązania analitycznego, oczywiście nawet wtedy, gdyby przyjąć, że silniki napędowe wytwarzają właściwy, stały moment. Jeśli jednak założymy, że obie niewyważone masy wirują ze stałą prędkością, możemy ocenić ustalony rucl wibratora. I tak, niechaj:
d, = Qt + d0; t3-2 = -Qt -i3-0
gdzie Q jest pulsacją kątową silników napędowych i - oczywiście - pulsacja h jest stała. Teraz równanie (10.4a) przyjmie postać:
Wyszukiwarka