51

94 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

Powyższe równanie, jako liniowe, można rozwiązać analitycznie. Niemniej jednak interesuje nas tutaj wyłącznie rozwiązanie asymptotyczne, lub inaczej mówiąc -rozwiązanie dla stanu ustalonego. Przewidujemy to rozwiązanie w postaci: x = x₀ +a-j, gdzie x₀ jest rozwiązaniem dla wymuszenia stałego pochodzącego od siły ciężkości, a x_l jest rozwiązaniem dla wymuszenia sinusoidalnie przemiennego. Teraz możemy napisać dla x₀:

^X° ~ k

oraz, wykorzystując rachunek symboliczny, dla x{.

2m„eQ^/

k - (m + 2m_e )Q² + JD_XQ Ostatecznie więc otrzymamy następującą postać:

jCos{Qt+$₀-y)    (11.6)

x(t) =

(m + 2m_e)g    2 meQ²

gdzie

y = a tan

Pulsację rezonansową wibratora wyznaczymy, obliczając maksimum amplitudy funkcji cosinus w wyrażeniu (11.6), zatem:

2m_aeQ"

^ -\j[k ~ {^m + 2m_e )0² j²-ł- {D_xQ.y

stąd

O = k

2k(m + 2m_e)-D²

(11.7)

Natomiast maksymalna amplituda drgań wibratora wyrazi się wzorem:

(11.8)

4 km_ee

D^4k(m + 2m_e)-D^

W rzeczywistych układach wibratory mają tak dobrane parametry, aby wykazywały charakter rezonansowy, zatem musi zachodzić silna nierówność:

2k(m + 2m_e))D²x (11.9)

Przykładowy przebieg charakterystyki rezonansowej przedstawiono na rysunku 48. Szczególną cechą tej charakterystyki jest jej mała zmienność po pewnym przekroczeniu pulsacji rezonansowej. Z powodu tej własności wibratory te pracują w obszarze nadrezonansowym. Wraz z obciążeniem takiego wibratora maleje bowiem nieco prędkość obrotowa silników napędowych, natomiast amplituda wibracji nie ulega praktycznie żadnym zmianom.

w = 314,1593

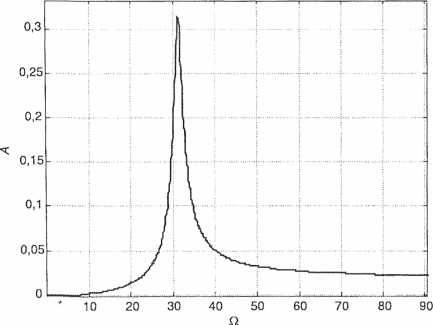
Rys. 48. Charakterystyka rezonansowa wibratora pionowego

Obecnie zajmiemy się stanami przejściowymi wibratora. Jak to już wcześniei było omawiane, model matematyczny mechanicznej części wibratora jest opisy-wany układem trzech równań różniczkowych nieliniowych drugiego rzędu. Ro/ wiązanie tego układu jest możliwe metodami numerycznymi. Zazwyczaj metody U'