52 53

Porównując zatem dyspersję różnych szeregów (mających to samo miano i zbliżony średni poziom cechy), należy dla każdego z nich obliczyć tę samą miarę zróżnicowania.

Odchylenie standardowe jest charakterystyką bardzo cenną i często wykorzystywaną w badaniach statystycznych. Jest ono precyzyjną i logiczną miarą zmienności, przy której inne miary możemy traktować jako drugorzędne. Odchylenie standardowe ma następujące właściwości:

1) jest wielkością obliczaną na podstawie wszystkich obserwacji w danym szeregu;

2) jego wartość nie zmieni się. jeśli liczebności szeregu wyrazimy w liczbach względnych (procentach) dostatecznie dokładnie ustalonych;

3) wartość odchylenia standardowego nic zmieni się, jeśli do wszystkich wartości zmiennej w szeregu dodamy pewną stałą liczbę;

4) jeżeli wszystkie wartości szeregu pomnożymy przez pewną stałą liczbę większą od zera. to odchylenie standardowe będzie również tylokrotnie większe.

Z odchyleniem standardowym wiąże się również tzw. reguła trzech sigm (odchyleń standardowych), według której w przypadku rozkładu normalnego (lub zbliżonego do normalnego) blisko trzecia część (31,73%) wszystkich obserwacji wartości zmiennej różni się t>d średniej arytmetycznej o więcej niż ±s. około jedna na 20 obserwacji przekracza tę średnią o wielkość ±2s, a tylko jedna na 370 obserwucji przekracza średnią arytmetyczną o ±3s.

Omówione dotąd miary dyspersji są miarami bezwzględnymi, gdyż wyrażamy je w takich samych jednostkach juk wartości badanej zmiennej. Nie pozwala to na porównywanie zmienności cech o różnych mianach. Nie można ponadto porównać pod względem tej samej cechy dwóch (lub kilku) zbiorowości będących na różnym poziomic, określonym np. średnią arytmetyczną czy medianą. Dlatego leż w analizie dyspersji powszechnie stosuje się względną miarę zróżnicowania — współczynnik zmienności.

Współczynnik zmienności jest ilorazem bezwzględnej miary dyspersji i odpowiednich wartości średnich. Jest on wyrużony w procentach. Ponieważ w analizie rozkładu wartości cechy korzystamy /. różnych miar zróżnicowania i różnych miar przeciętnych, można obliczać współczynniki zmienności kilkoma metodumi:

V * - • KM). (2.32)

.?

(2.34)

— • 100,

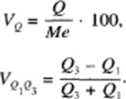
(2.33)

(2.35)

Współczynniki zmienności określone wzorami (2.32) i (2.33) noszą nazwę klasycznych, a pozostałe dwa — pozycyjnych.

Współczynniki zmienności informują o sile dyspersji. Duże ich wartości liczbowe świadczą o niejednorodności zbiorowości.

Poniżej podajemy przykład praktycznego zastosowania współczynnika zmienności dla celów porównawczych.

Średnie miesięczne wpływy za świadczenie usług noclegowych w trzech losowo wybranych hotelach A,B \C były równe: x_A — 600 tys. zł, x_B — 300 tys. zł, x_c — 500 tys. zł. Odchylenia standardowe wartości sprzedanych usług wynosiły: s_A = 110 tys. zł, = 90 tys. zł i s_c = = 120 tys. zł. W którym hotelu występuje największa dyspersja miesięcznych wpływów za świadczenie usług noclegowych?

Podane w tym przykładzie wartości odchyleń standardowych nie mogą być podstawą do wyciągania wniosków o sile dyspersji ze względu na znaczne różnice w średnim poziomie wpływów w poszczególnych hotelach. Do tego celu należ.y zastosować współczynnik zmienności określony wzorem (2.32). Podstawiając odpowiednie wartości liczbowe otrzymujemy:

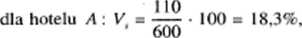
dla hotelu B: V = — • 1(X) = 30,0%,

' "J AA

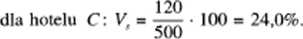
l ak więc największe względne zróżnicowanie miesięcznych wpływów za świadczenie usług noclegowych miało miejsce w hotelu B, najmniejsze zaś w hotelu A.

Wyszukiwarka