57
106 A.S. .l;ij>icllo. Systemy elektromechaniczne dla deku vhó\\
106 A.S. .l;ij>icllo. Systemy elektromechaniczne dla deku vhó\\
tris(x)= lim
Hm arcsin[psin(x)]
p-KO arcsin(p)
I)o obliczeń numerycznych, a także ze względu na szybkość pracy półprzewodnikowych elementów przełączających w miejsce poszukiwania granicy - jak to zostało zapisane w powyższym wzorze - podstawiana jest wartość p bliska, lecz mniejsza od jedności. Oczywiście, w miejsce funkcji „com”, jako spełniający warunki Dirichleta, można wstawić szereg Fouriera, jednak w takim przypadku każda zmiana szybkości działania elementów półprzewodnikowych wymaga zmiany liczby wyrazów szeregu lub oznacza godzenie się ze zmianą dokładności obliczeń. W ogólności, w formach krzywoliniowych, zwanych też serrafilowymi, nie ma związku między dokładnością a wielkością (długością) wyrażenia aproksymują-cego, nie występuje również efekt Gibbsa. Największym mankamentem tych form jest brak ogólnych formuł matematycznych, pozwalających na zapisanie za ich pomocą zadanych funkcji okresowych.
Powyższe relacje jako związki między pochodnymi współrzędnych można uważać za więzy kinematyczne. Ponieważ równania te są niecałkowalne, więzy takie nazywane są więzami nieholonomicznymi. Modyfikując funkcje potencjału kinetycznego (L) równaniami więzów, otrzymamy:
i = ł (4 + d,)Q2 + MąfQ + i + {JÓ2
Po podstawieniu powyższego wyrażenia do równań (2.12) otrzymujemy:
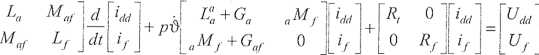
(12.1a)
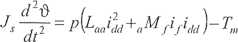
(12.Ib)
gdzie
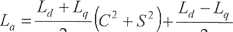
2
2
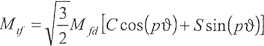
[(c2 - S2 )cos(2pd) + 2CS sin(2/?$)]
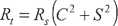
l.m (/,, -Lj2CScos(2p-&)-{c2-S2)sin(2/>d)]
,Mf = }j^M/d[Scos(pd-)-Csm
G„ =±t^{CCd+SSd) + -^^[(CCd-SSd)cos(2pV)+(CSd + SCd)sin(2p
Gy = Mf, [Cdcos (pd)+sin (pd)]
C = -j|com(pd-Tl)
■Jl
5 =-y-[com(pd - Tl -7t)-com(piJ - Tl) -1 Jt J C - 8C .
" 3(p*-n)
^ 3(p$-ti)
Na rysunkach 58a i b przedstawiano kształt funkcji C i 5 będących matematyczną emanacją działania falownika prądu traktowanego jako urządzenie wprowadzające więzy nieholonomiczne liniowe. Zauważmy, że funkcja C jest właściwie funkcją „com”, tyle tylko, że pomnożoną przez pewną stałą.
Aby lepiej zrozumieć powody wytwarzania przez maszynę bezszczotkową prądu stałego momentu elektrycznego o znaczącej składowej przemiennej, na rysunkach 59 i 60 przedstawiono przebiegi tych współczynników w funkcji obrotu wirnika, które mają zasadniczy wpływ na kształt tego momentu. O ile włączając w odwód pośredniczący falownika dławik, można „wygładzić” prąd w tym obwodzie, to na zmienność współczynników aMf oraz Laa dla danej konfiguracji
uzwojeń stojana nie mamy żadnego wpływu.
Rozważymy teraz system elektromechaniczny złożony z maszyny bezszczot-kowej prądu stałego, pracującej w układzie obcowzbudnym, napędzającej przez elastyczny wał organ roboczy o zadanym momencie bezwładności. Niech stojan silnika będzie zamocowany do podłoża w elastyczny sposób, tak aby mógł on wykonywać jedynie w ograniczonym zakresie ruch obrotowy w płaszczyźnie ruchu
Wyszukiwarka