58 59

Stosunek pola zawartego między linią równomiernego rozdziału a krzywą koncentracji I x>renza («) do pola połowy kwadratu nosi nazwę współczynnika koncentracji Lorenza:

k

a

5000

(2.47)

Współczynnik koncentracji jest miarą niemianowaną i zawiera się w przedziale: 0 < k < 1. Jeśli k = 0. to mamy do czynienia z brakiem koncentracji, przy k = I zaś występuje koncentracja zupełna.

Praktyczny sposób postępowania przy pomiarze siły koncentracji metodą graficzną i analityczną zaprezentujemy na przykładzie (tablica 7).

Tablica 7. Liczba ludności w gminach w Polsce w 1977 r.

Gminy o liczbie ludności (w lys.)	Liczba gmin	Liczna liczba ludności^-1(w ty$.)	Częstości względne		Skumulowane częstości względne
			liczby gmin	łącznej liczby ludności	liczby gmin	łącznej liczby ludności
powyżej 2	IS	23.4	0.7	0.2	0.7	0.2
2- 5	490	1 972,5	23,7	13.3	24.4	13.5
5- 7	663	3951.3	32,0	26.6	56.4	40.1
7-10	551	4 551.0	26.6	30.6	K3.0	70,7
powyżej 10	351	4 364,3	17.0	29.3	100.0	100.0

*    licithc ludhofai w pouuiKgńtaych pncd/iłłMłl puduw ilu pabziwlr iŁin;i'll inilvwiik*ilii)Ui, gdyż

Kooouoe /umykuuic pive<l/u>Vw i Kor/ytlunie /c .4rc«łk<W kkii pm»:ulzili>ł>y ilu ilnfyiti hlęiuv*

Źródło: Ft*zniX iSr/m/yrafn cm 197$, u. 7—8.

Już na podstawie pobieżnej analizy danych zawurtych w tablicy 7 można stwierdzić, że zachodzi tu zjawisko koncentrucji liczby ludności w gminach. Odczytując parami odsetki liczby gmin i odsetki łącznej liczby ludności zauważamy bowiem dość znaczne różnice. Występowanie koncentracji potwierdza również wykres wielohokti koncentracji (rys. 7).

Do obliczenia współczynnika koncentracji /a pomocą w/oru (2.47) niezbędna jest znajomość powierzchni a. W tym celu należy uprzednio ustalić powierzchnię znajdującą się poniżej kr/.ywcj koncentracji Lorenza. Dokładne ustalenie tej powierzchni wymogu ziuijomości analitycznej postaci funkcji krzywej koncentracji. W badaniach empirycznych powierzchnię tę znajduje się w sposób przybliżony jako

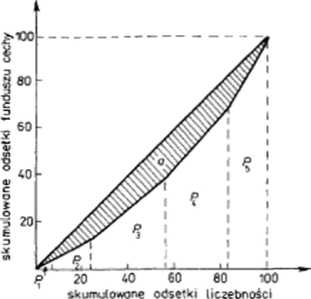
Rys. 7. Wielobok koncentracji

sumę pól trójkąta i trapezów (por. rys. 7). Figur tych jest tyle. ile jest wierszy w szeregu.

Powierzchnię pod krzywą koncentracji można zatem obliczyć jako:

P = P, +

im 2

(2.48)

gdzie: P, — pole trójkąta; P, — pole i-tego trapezu.

Korzystając ze znanych wzorów na pole trójkąta i trapezu otrzymujemy:

P,=

P₃ =

0.2 • 0.7 2

0.2+ 13,5

0.070.

• 23,7 = 162,345,

P, =

13.5 + 40.1

32 = 857.6.

P$ ⁼

40.1 + 70.7 2

70.7 + 100 2

■ 26.6 = 1473.64. • 17 = 1450,95.

59