70

lub w postaci czasowej:

		(k2 - CO^2 J2)	r + (coD)^2 sin(co/ + a -		-P)
1	— {j[k2 + J2k\ + J2k		'■) )co^2 + kjt2 ]	f+M^2|	1 + to 'T to

(14.2)

l»dzie

a = arctg

f «p )

[k₂-(D²J₂J

P

= arctg——_T

J_lJ₂<Si

coD^-^+^y]

— {J\k₂ + J₂k\ + J₂k₂ )co² + k\k₂

Teraz możemy napisać wyrażenie na współczynnik przenoszenia, za który uważa się iloraz amplitudy momentu przenoszonego przez sprężynę k_x do amplitudy momentu wymuszającego:

P =

k^(k₂-u²J₂j + {®D)²

yj\jiJ₂Ol)⁴ - i_yJJi₂ + J₂k_{ + J₂k₇ )ftr + kjc₂] ²+ (coD)" [fcj ~{j\ + J₂ )co²

(14.3)

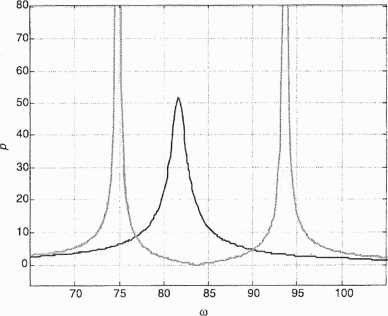
Rys. 89. Zależność wibroizolacji momentowej od pulsacji kątowej wymuszenia dla różnych współczynników tłumienia w dużym zakresie jej zmian

Na rysunku 89 przedstawiono odcieniami szarości zależność współczynnika wibroizolacji momentowej w funkcji pulsacji wymuszenia dla różnych współczynników tłumienia. Odcieniem średnioszarym zaznaczono przebieg dla zerowej wartości stałej tłumienia, jasnoszarym dla —— = 1, natomiast ciemnoszarym -^- = 100.

Analiza tych przebiegów wskazuje, że zbyt duży współczynnik tłumienia powoduje nawet wzrost (i to znaczny) siły przenoszonej na układ mocujący (ścianą). Natomiast współczynniki tłumienia mały i zerowy, jak to można wywnioskować z rysunku 90, mają bardzo wąski przedział zmian częstotliwości, w którym współczynnik wibroizolacji jest mniejszy od jedności. Stąd opisany układ może być wykorzystywany jedynie w takich systemach drgających, w których częstość momentu wymuszającego zmienia się w bardzo małym przedziale.

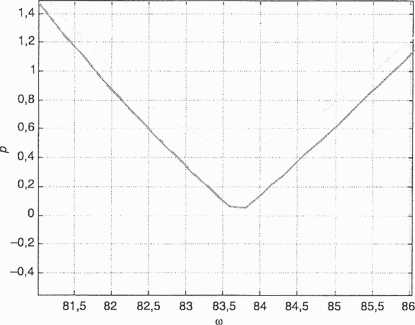
Rys. 90. Zależność wibroizolacji momentowej od pulsacji kątowej wymuszenia dla różnych współczynników tłumienia w małym zakresie jej zmian

Istnieje ponadto wiele innych metod eliminacji drgań, zarówno biernych, jak i czynnych, jednak ze względu na zakres niniejszego podręcznika nie będą tu omawiane.

#