73

I W

A.S. Jagiełło, Systemy elektmmeilitnitc.uie dla elektryków

W przypadku równania (15.5b) możemy napisać:

W wyniku zaznaczonych działań otrzymujemy:

i /,„	0	0	^0 1	w r°	0	0	^0 Ul \^R-	0	0	Oj/ol	'i/.l
0 0	Ld 0	0 I,	i/i«. 0	d U, i jo \ dtUi I ' ' 0	0 4/	-L(/ 0	o M o JĘm. ! i, l i o	R, 0	0 Rs	o o -	u A ^u*
0	l/I".	0	h .	i L'/j [0	0	0	o 14 [0	0	0		Vj\

(15.6)

Postępując analogicznie z równaniem (15.3b), otrzymuje się:

⁼    plliMJSs + ~^r‘.    (¹⁵⁷>

^! i	k	i 4i	i V2	Y
=Ą	COs(/7l})	cos(pd-j7t)	cos(pń-j7t)	h
J	[-sin(pd)	-sin(/?$-j7t;)	-sin^p-d-yT^j	_h_

gdzie

oraz w analogiczny sposób przekształconą macierz napięć trójfazowych zasilających uzwojenia stojana:

V	i	- 1 _L _L 1 41 4i 42		'u;
u,	= V¥	COs{]X&) COs(pń-fTc) COs(pń-y7l)		U2
ł		-sin(pń) -sin(pń--=-7t) -sin(pi5--f 7c)		U,.

Dla symetrycznego trójfazowego zasilania napięcia te przyjmują wartość:

r^oi	1	0
v.\	=SuJ	cos(co? - ptl)
		I sin(atf - pi3-)J

gdzie U_ph jest wartością skuteczną napięcia fazowego zasilającego maszynę synchroniczną.

15.2. MASZYNA SYNCHRONICZNA OPISANA ZA POMOCĄ QUASI-WSPÓŁRZĘDNYCH „0 a (3”

Opis matematyczny maszyny synchronicznej za pomocą ąuasi-współrzędnych „0 d ą” jest bardzo wygodny do analizy obliczeniowej w przypadku maszyny pracującej samotnie. Sprawa się jednak bardzo komplikuje w sytuacji współpracy kilku maszyn zasilanych ze wspólnej, elastycznej sieci. Powodem tego jest fakt, że prądy i napięcia każdego z silników opisanych takim modelem zależą od chwilowego położenia własnego wirnika. W takim przypadku stosuje się najczęściej inne modele. Jednym z nich jest model matematyczny wykorzystujący współrzędne „0 a (3”. Macierzą przekształcenia jest tu macierz Clarka o postaci:

Teraz postępowanie jest analogiczne jak w przypadku transformacji Parka, tyle tylko, że macierz Clarka nie sprowadza do postaci diagonalnej macierzy indukcyj-ności stojana. W rezultacie tych działań otrzymuje się:

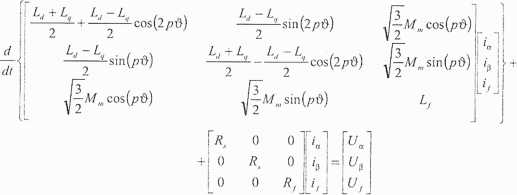
(15.9a)

2