47

86 A.S. Jagiełło, Systemy elektromechaniczne dla elektryków

jest to dogodne, zwłaszcza w przypadku, gdy do tłoka jest przyłożona siła o charakterystyce zależnej od położenia tłoka wewnątrz cylindra. Wobec powyższego równanie więzów (9.2) nieco zmodyfikujemy:

x = l + r — r cos(f)-$₀)-^//² -r² sin²(i3-^₀)    (10.3)

gdzie \ jest kątem, przy którym położenie tłoka wewnątrz cylindra uważamy za zerowe.

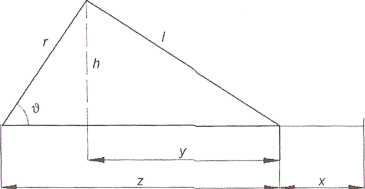
Rys. 40. Pomocnicza konstrukcja pozwalająca na określenie równania wiązów występujących w korbowodzie

Różniczkując obustronnie względem czasu równanie (10.3), otrzymamy relacje między prędkościami układu:

rsin(i3-i3₀) +

r² sin2(i3--'0-₀) 2^['² - r² sin² (d -    )

(10.4)

Po podstawieniu równań (10.3) i (10.4) do funkcji Lagrange’a (10.1) otrzymamy:

___sin² 2(0--i3₀)

Jl²-r² siif(d-i3₀) "⁴(/²-r²sin²(d-d₀))

d²

r    1    «•    2

L— = — <J+mr 2

(10.5)

Po podstawieniu funkcji Lagrange’a (10.5) do równania Lagrange’a drugiego rodzaju:

d_ dL dL _ j dt

otrzymamy równanie dynamiki korbowodu:

rsin(fl)sin 3M    r² sin² 2(d)

\ J + mr²\ sin²($)+

V/²-^sin²(d)    4(/² — r² sin²(iS

V/² —r² sm²(i)[sin(3i)₊c_0s(2l)sin(d)]₊ ^

sinM +/■

2y/² — r² sin²(fl)

/² -r²sin²(d)

gdzie:

■mr ty

\r^2 2sin(4i3-)[/'	^! - r^2 sin^21	i#)]	\+r^2 sin^3(2i3-)|
l^4 1	7^2 - r^2 sin	^2(«)]		1

(10.6)

7"_nap - moment napędowy.

Powyższa postać modelu matematycznego korbowodu nie jest dogodna do obliczeń numerycznych, zwłaszcza za pomocą standardowych metod rozwiązywania równań różniczkowych. Aby uzyskać pożądaną postać, należy wykonać różniczkowanie względem czasu pierwszego członu w równaniu (10.6), w wyniku czego otrzymamy:

J + mr²

sin

\ rsin(fł)sin2(i3-) r² sin² 2(«) V/²-r²sin²(i})    4(/²-c²sin²(d))

+ ^mr²b²\sin[2($)|+ r

d²$

dr

V/²-r²sin²(^)[sin(3^)+cos(2^)sin(i5)]+^r .^Sin '^2x

2yjl² -r²

/²-r² sin² (^)

2'ó)sin(i)) |

-r sin h)i

, i mrwld2sin(4d|/²-i-²sin²(d)]+>-²sm³(2d)]_

²    [4    [/² -r² sin²(d)f    j

W dalszych rozważaniach przyjmiemy, że korbowód ten jest napędzany przez silnik indukcyjny trójfazowy, którego model matematyczny jest dany równaniami (8.1). Równania te zatem powtórzymy: