Image0022 BMP

Na powierzchni naładowanego ciała metalowego znajduje się ładunek powierzchniowy o gęstości o. Ponieważ we wnętrzu ciała metalowego nie ma pola elektrostatycznego, więc w zależności (2.20) należy przyjąć D„₂ —0. Wobec tego składowa normalna £►„=/)„, w dielektryku bardzo blisko powierzchni ciała wyraża się wzorem

D„=<r.    (2.21)

Zazwyczaj na powierzchni granicznej dwóch dielektryków nie ma ładunku powierzchniowego. Podstawiając (7=0 do wzoru (2.20), otrzymujemy

0„_t =£>„*,    (2.22)

czyli

Djcosa, =D₂cosa₂,    (2.23)

gdzie: «,, cc₂ są kątami, jakie tworzą odpowiednio wektory D, i D₂ z normalną do powierzchni granicznej.

Jeżeli na powierzchni granicznej środowisk nie ma ładunku elektrycznego, to składowa normalna wektora indukcji elektrycznej jest ciągła w punktach tej powierzchni.

Składowe normalne E_nl, E„₂ natężenia pola elektrycznego są nieciągłe w punktach powierzchni granicznej środowisk, bowiem na podstawie zależności (2.22) otrzymujemy

(2.24)

(2.25)

^G1 Enl ^{= [i}2 E-n2 j

czyli

E_nj _ ^a2 £.2 Zi

W celu otrzymania warunku granicznego dla składowej stycznej natężenia E pola elektrycznego rozpatrzymy krzywą zamkniętą o postaci prostokąta, którego dwa boki o długości dl są równoległe do powierzchni granicznej i znajdują się w różnych środowiskach (rys. 2.5). Niech E_n i E_t2 oznaczają składowe styczne natężenia pola elektrycznego bardzo blisko powierzchni granicznej, odpowiednio w środowisku górnym i dolnym. Napięcie wzdłuż rozpatrywanej krzywej zamkniętej wynosi E_tl dl— E_t2 dl, bowiem napięcia wzdłuż obu wysokości zanikają w granicy. Ponieważ napięcie wzdłuż krzywej zamkniętej równa się zeru, więc

E_n=E_t2,    (2-26)

czyli

fitsin*, a=£₂^si^nflE2 ■    (2.27)

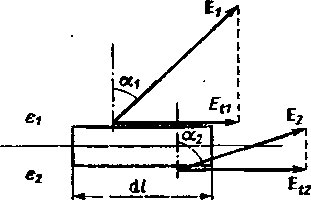
Rys. 2.5. Elementarna krzywa zamknięta przy powierzchni granicznej dwóch środowisk

Oznacza to, ic składowa styczna nntęMuu pola elektrycznego jest ciąglu w punktach powierzchni granicznej.

Składowa styczna indukcji elektrycznej w punktach powierzchni granicznej jest nieciągła, bowiem na podstawie wzoru (2.26) otrzymujemy

D*

El

D_t2

H

a stąd

(2.28)

0,1 c₂

Dzieląc stronami równania (2.27) i (2.23) przez siebie, otrzymujemy

£_t    Ei

czyli

tga₂ e₂

Wzór ten wyraża tzw. prawo załamania linii poła elektrycznego w punktach powierzchni granicznej (rys. 2.6).

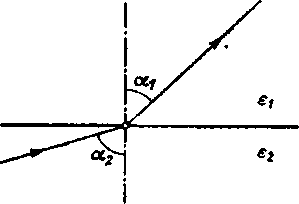
Rys. 2.6. Załamanie linii pola elektrycznego na granicy dwóch środowisk

2.4. Równanie Poissona i Laplace’a

2.4.1. Pole trójwymiarowe

Rozpatrzymy pole elektrostatyczne w jednorodnym środowisku o przenikalności elektrycznej c=const.

Podstawiając D=cE do wzoru div D'=/?, otrzymujemy