skanuj0024 (13)

Dla ciał 2 i 3

Dla ciał 3 i 4.

^2^2 ^— ♦ R₂<p₂=2Rtf_y

(*3 ⁺r₃)<P_i =j₄*

(^Ri+r₂)Vi=x₄.

(D-18.57)

(D-18.58)

Równanie ruchu ciała 2

Ponieważ interesuje nas równanie ruchu ciała 2, wyraźmy nieznane wielkości x_{,(p₃,x₄ przez (p₂. Korzystając ze związków geometrycznych (D-18.56) do (D-18.58), otrzymamy

=^r2<Pi>

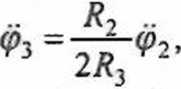
*4 = (^R1 + ^r3 )<P3 = (*3 + ^r3 )^-<P2 •

(D-18.59)

Po uwzględnieniu zależności (D-18.59) w równaniach (D-18.5), (D-18.5), (D-18.5) i (D-l 8.55) otrzymamy układ równań

^ml ^r2 $2 ~ ^R°2 “ ^R12 >    (D-l 8.60)

'”4(^R3+'-3h£r<P2=S₄₃-S₄°₃,    (D-18.61)

zk₃

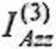
= -G₃R₃ sin 10° - G₃f cos 10° - S_3A (R₃ + r₃) + S₂₃ 2/?₃,

2 • R₃

(D-l 8.62)

/^<p₂ =M+S_2lr₂-S_2iR₂.    (D-l 8.63)

Z równań (D-18.60)-(D-18.62) otrzymamy

^sn^=S2i=SZ\~'»_lr₂$2>    (D-l 8.64)

231