P7270361

Miejsce na naklejkę z kodem (Wpisuje zdający przed rozpoczęciem pracy)

cm

Zestaw 1.

KOD ZDAJĄCEGO

EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII

Arkusz II

ARKUSZ II ROK 2005

(dla poziomu rozszerzonego)

Czas pracy 120 minut

Instrukcja dla zdąjącego

1. ” Proszę sprawdzić, czy arkusz egzaminacyjny zawiera odpowiednią

liczbę stron. Ewentualny brak należy zgłosić przewodniczącemu zespołu nadzorującego przebieg egzaminu.

2. Proszę uważnie czytać wszystkie polecenia.

3. ’ Rozwiązania i odpowiedzi należy zapisać czytelnie w miejscu na to

przeznaczonym przy każdym zadaniu.

4. W rozwiązaniach zadań rachunkowych trzeba przedstawić tok rozumowania prowadzący do ostatecznego wyniku oraz pamiętać o podaniu jednostek obliczanych wielkości.

5. W trakcie obliczeń można korzystać z kalkulatora.

6. " Proszę pisać tylko w kolorze niebieskim lub czarnym; nie pisać

ołówkiem.

Za rozwiązanie wszystkich zadań można otrzymać łącznie 50 punktów

7. Nie wolno używać korektora.

8. Błędne zapisy trzeba wyraźnie przekreślić.

9. * Brudnopis nie będzie oceniany.

10. Obok każdego zadania podana jest maksymalna liczba punktów, którą można uzyskać za jego poprawne rozwiązanie.

11. Do ostatniej kartki arkusza dołączona jest karta odpowiedzi, którą wypełnia egzaminator

Życzymy powodzenia!

Punkty te nie dotyczą tej publikacji, ale pojawią się w arkuszach na egzaminie maturalnym

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

ARKUSZ - II A

Zadanie 1. Kulka na nitce [14 pkt]

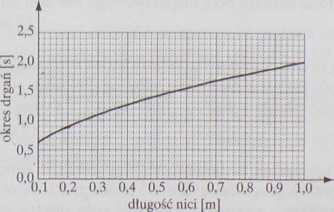
Na wykresie przedstawiono zależność okresu drgań niewielkiej ołowianej kulki o masie 1 g,. zawieszonej na jedwabnej nici, od długości tej nici. W obliczeniach pomiń wpływ powietrza.

a) Oblicz wartość przyspieszenia ziemskiego w miejscu, w którym znajdowało się wahadło.

Potraktuj ten układ jak wahadło matematyczne. (3 pkt)

b) Oblicz wartość siły napięcia nici w chwili przechodzenia kulki przez położenie równowagi. Maksymalne wychylenie od pionu podczas drgań tego wahadła wynosiło 60°. W obliczeniach przyjmij, że nitka ma długość 1 m, a wartość przyspieszenia ziemskiego wynosi 10

(4 pkt)

c) Oblicz wartość prędkości, jaką należałoby nadać ołowianej kulce zawieszonej na nici i poruszającej się w płaszczyźnie poziomej, aby nić o długości 25 cm przez cały czas była odchylona od pionu o kąt 45°. Przyjmij wartość przyspieszenia ziemskiego równą 10

(3 pkt)

d) Oblicz minimalną wartość prędkości, jaką należałoby nadać kulce w jej najniższym poło

żeniu, aby mogła zatoczyć w płaszczyźnie pionowej okrąg o promieniu 0,5 m. W obliczeniach przyjmij wartość przyspieszenia ziemskiego równą 10 -Sk (4 pkt)

s¹

Zadanie 2. Elektron w polach elektrycznym i magnetycznym [21 pkt]

U[ kV]

W pewnym eksperymencie przyspieszony w polu elektrycznym elektron został skierowany w obszar jednorodnego pola magnetycznego, gdzie poruszał się ruchem jednostajnym po okręgu. Na wykresie przedstawiono zależność promienia okręgu, po którym poruszał się elektron, od napięcia przyspieszającego. W obliczeniach pomiń wpływ grawitacji i efekty relatywistyczne.

a) Oblicz wartość indukcji tego pola magnetycznego.

(5 pkt)

b) Oszacuj długość fali de Broglie’a elektronu poruszającego się w tym polu magnetycznym po okręgu o promieniu 4 mm. (4 pkt)