Slajd31 out
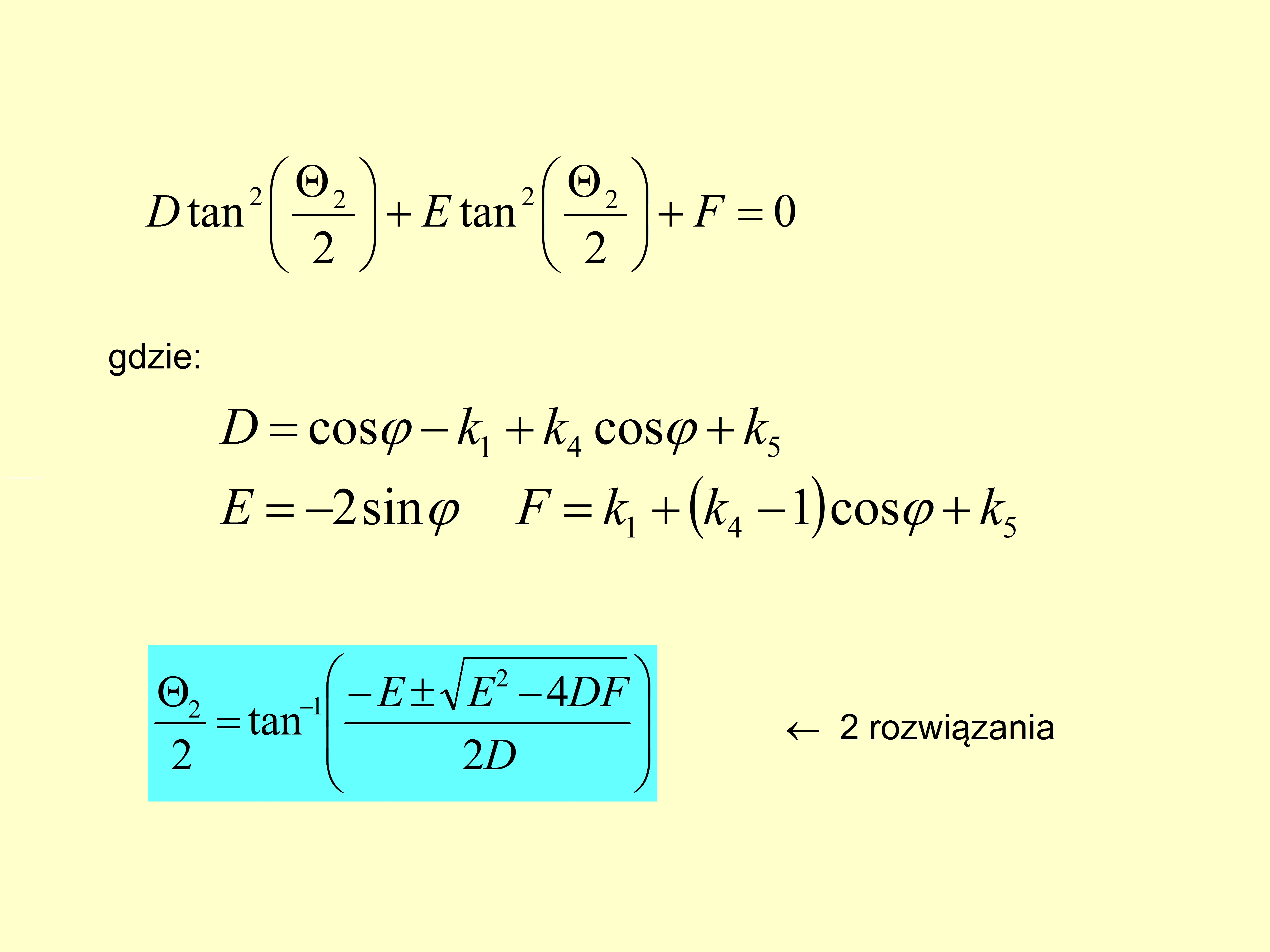
Z) tan
|
2 2 J |
+ E tan2 |
2 J |
+ F = 0
gdzie:
D = cosę -k{+kĄ cosę + k5 E = -2smę F = kl+(k4- l)cosę? + A;5
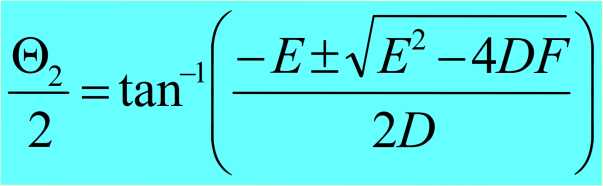
<- 2 rozwiązania
Wyszukiwarka
Podobne podstrony:
Slajd29 out A tan 2 J + 5 tan 2 J + C = O gdzie:A = cos (p~k] — k2
Slajd30 out Podobna droga do 02 acos^ + ź>cos@2 -d = ccos©3 2 <3sin^ + osin©2 = csin©3 (acos (
Slajd31 out (2) ABCK~Abck BC BK KB =-=-= . bc bk kb PODOBIEŃSTWO członu BCK i planu bek D
Slajd35 out PODOBIEŃSTWO członu i planu aABCK ~ Abck
Slajd33 out K+ a CB ^ n . ^ t ^ n . ^ t . ^ n . ^ t aC+aC-aB+aB+aCB+ aCB a U Pgdyż
45492 Slajd39 out aC + aC“aB+aB+ aCB aCB aCB = 8j • AB = O, gdyż c, = O — = 0, gdyż p= oc P = 2<o
75435 Slajd36 out Przykład 2
Image241 Z Pi* = 0 ^Z P» = RD Sil1 Ó>~ RS sin a = 0 2-1 2-1Z pif =0 Z pi? = rd cos k j cose = o
Image4762 , + Xxl2™<P2 <p - arc tg- xKi C0S<Pi + xk2 cosę?2
Image4873 p = -UJ* cosę? =1 1 2 1 2 —Re (77/*) = -/m2R = -yM3G
więcej podobnych podstron