img047 (33)

52

52

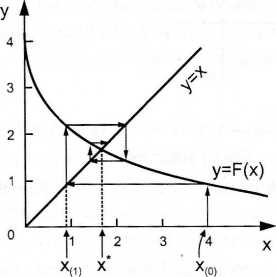
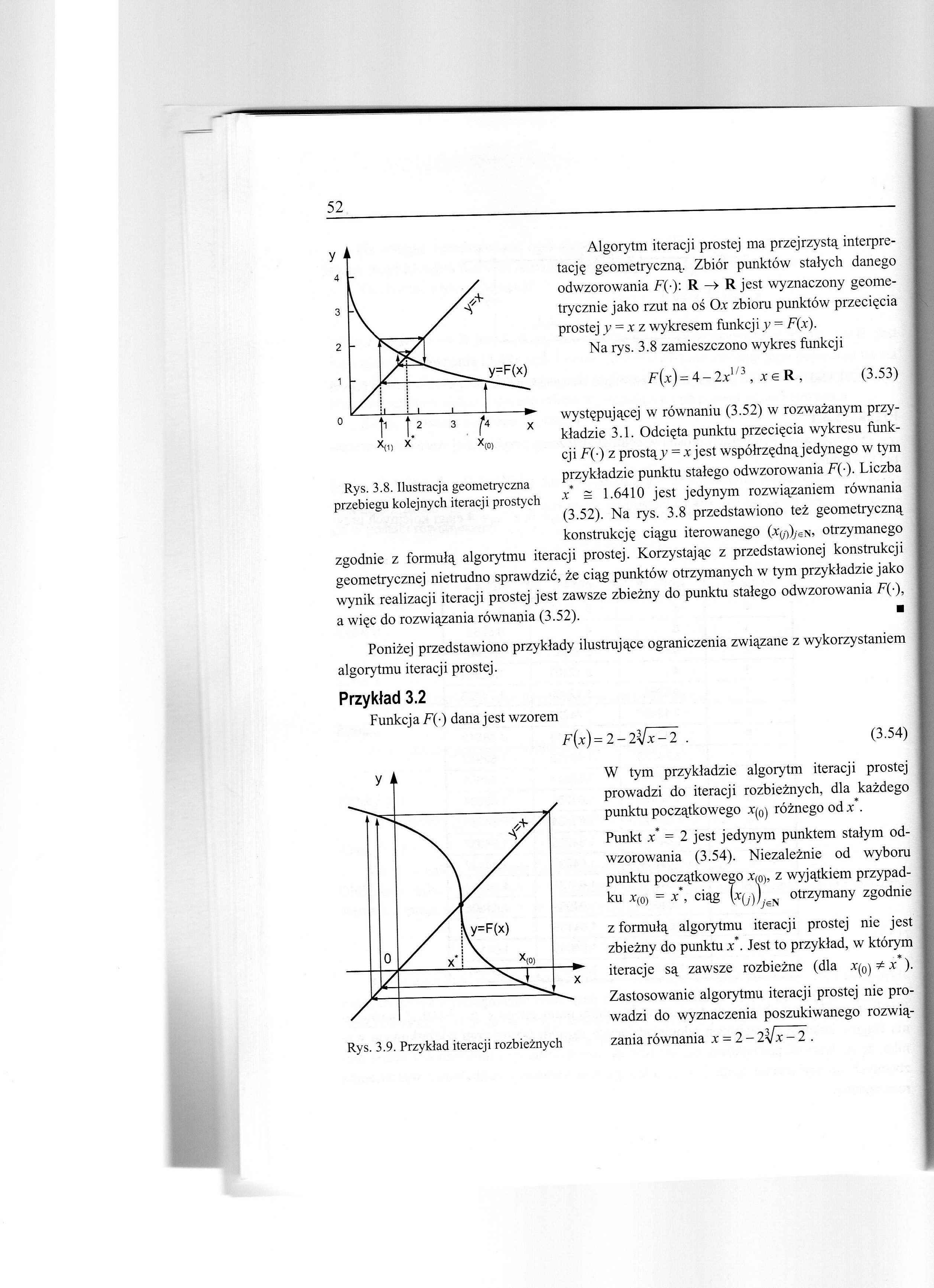
Rys. 3.8. Ilustracja geometryczna przebiegu kolejnych iteracji prostych

Algorytm iteracji prostej ma przejrzystą interpretację geometryczną. Zbiór punktów stałych danego odwzorowania F(-): R —> R jest wyznaczony geometrycznie jako rzut na oś Ox zbioru punktów przecięcia prostej y = x z wykresem funkcji y = F(x).

Na rys. 3.8 zamieszczono wykres funkcji

(3.53)

F(x)=4-2x^1/3, x e R .

występującej w równaniu (3.52) w rozważanym przykładzie 3.1. Odcięta punktu przecięcia wykresu funkcji F(-) z prostąy = x jest współrzędnąjedynego w tym przykładzie punktu stałego odwzorowania F(-). Liczba x* = 1.6410 jest jedynym rozwiązaniem równania (3.52). Na rys. 3.8 przedstawiono też geometryczną konstrukcję ciągu iterowanego (x_w)_/-_6N, otrzymanego zgodnie z formułą algorytmu iteracji prostej. Korzystając z przedstawionej konstrukcji geometrycznej nietrudno sprawdzić, że ciąg punktów otrzymanych w tym przykładzie jako wynik realizacji iteracji prostej jest zawsze zbieżny do punktu stałego odwzorowania F(-), a więc do rozwiązania równania (3.52).    ■

Poniżej przedstawiono przykłady ilustrujące ograniczenia związane z wykorzystaniem algorytmu iteracji prostej.

Przykład 3.2

Funkcja F(-) dana jest wzorem

F(x)=2-2Vx-2 .    (3.54)

W tym przykładzie algorytm iteracji prostej prowadzi do iteracji rozbieżnych, dla każdego punktu początkowego x(₀) różnego od x .

Punkt x = 2 jest jedynym punktem stałym odwzorowania (3.54). Niezależnie od wyboru punktu początkowego X(₀), z wyjątkiem przypadku x₍₀) = x*, ciąg (x(₇))^_eN otrzymany zgodnie

z formułą algorytmu iteracji prostej nie jest

zbieżny do punktu x*. Jest to przykład, w którym

• *

iteracje są zawsze rozbieżne (dla x(₀) ^ x ).

Zastosowanie algorytmu iteracji prostej nie prowadzi do wyznaczenia poszukiwanego rozwiązania równania x = 2-2Vx-2 .