skanuj0010 (282)

to wyznaczyć kolejno 2frU, 3JO, 4JU. znajomość tych Aioiikftw obrotu umożliwia sporządzenie planu przemieszczeń obróconych (pełnego planu pokazanego na rysunku).

Z lokalizacji środków wynika, że tarcza 1 jest nieruchoma. Nadając możliwe przemieszczenie obrócone punktowi A (AA") i wykorzystując twierdzenia o ruchu płaskim dla tarcz, kolejno można wyznaczyć BB", CC", DD", HE" i FF"! Więź podporowa R (przerywana), ze względu na swój kierunek uniemożliwia realizację przemieszczenia FF" (możliwe przemieszczenie obrócono to przesunięcie poziome). Otrzymujemy zatem sprzeczność w możliwości ruchu punktu F; świadczy to o geometrycznej niezmienności schematu.

Nic jest to jedyny wariant dowodu geometrycznej niezmienności schematu przy tym podejściu, możliwe bowiem jest myślowe usunięcie innej więzi, podporowej lub wewnętrznej. Wniosek końcowy jest następujący: wobec zachowanego kryterium jakościowego geometrycznej niezmienności i spełnionego warunku ilościowego — układ jest statycznie wyznaczałny (izostatyczny).

Geometryczną niezmienność układu (po sprawdzeniu warunku ilościowego) można zbadać metodą analityczną. W tym celu dzielimy układ na zbiór tarcz izolowanych (4 tarcze, a w miejsce usuniętych więzi przyjmujemy stosowne niewiadome reakcje — R> H, V_t W i interakcje (siły wewnętrzne) — T, N, Z, M, S, 17, K, F.

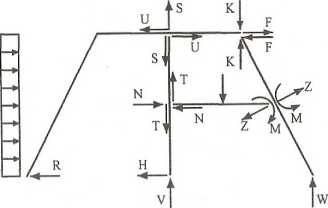
Dla każdej tarczy możemy napisać 3 klasyczne (lub wariantowe) równania równowagi Otrzymujemy zatem układ 12 równań o 12 niewiadomych.

W celu zbadania geometrycznej niezmienności układu badamy wyznacznik przy niewiadomych.

Rozmiar zadania można zmniejszyć rozważając poniższy schemat obliczeniowy (jeden z możliwych).

Należy zwrócić uwagę, że w zadaniu tym nie ma możliwości niezależnego wyznaczenia wszystkich reakcji.

Należy je wyznaczyć łącznie z grupą interakcji (w tym przypadku T, N; po otwarciu komory otrzymujemy graf otwarty, co bardzo ułatwia obliczanie sił wewnętrznych) wykorzystując trzy warunki równowagi oraz 3 warunki konstrukcyjne:

guma rzutów wszystkich sil na oś X równa się zero (ZX = 0)

R+H-2-8 = 0,

suma rzutów wszystkich sił na oś Y równa się zero (£7 = 0)

V+W- 8 = 0,

Numa momentów wszystkich sił względem bieguna i równa się zero (£Af _t m 0) 87+2*8*4—8*5 = 0,

siła w kierunku osi rj równa się zero (P_n = 0)

T-2/t/Ś+N- 1/V5-8-2/Vs = 0, moment gnący w punkcie 2 równa się zero (Af₂ = 0)

H'S—N’4 = 0,

moment gnący w punkcie 3 równa się zero (Af₃ = 0)

- W-4+T-4+N-4S-1 = 0.

Macierzowy zapis układu równań ma postać A-W„+W_w = G,

gdzie

- wektor niewiadomych W„ = (R, H, V, W, T, N)^T,

⁸’²⁴’-^’⁰-

-(■

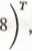
wektor wyrazów wolnych W_y

16,

macierz współczynników		przy niewiadomych
	'l 1	0	0	0	0
	0 0	1	1	0	0
	0 0	8	0	0	0
A —	0 0	0	0	2/y/5	1A/5
	0 0	0	0	0	-4
	.0 0	0	-4	4	4

41