skanuj0014

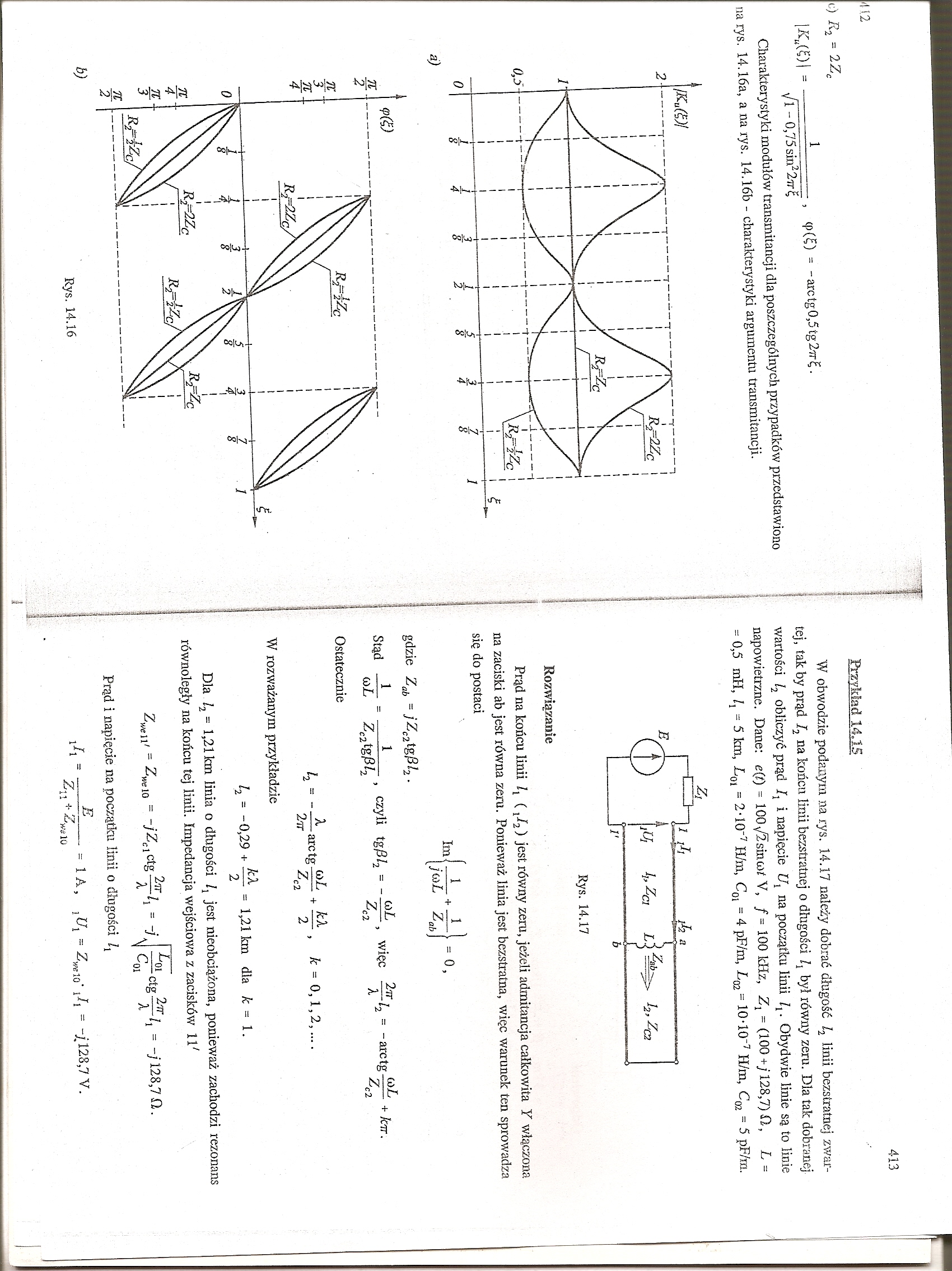
|jK«(OI = - -........... <P(£) = -arctg0,5tg2ir£.

y/l - 0,75 sin² 2ir£

Charakterystyki modułów transmitancji dla poszczególnych przypadków przedstawiono na rys. 14.16a, a na rys. 14.16b - charakterystyki argumentu transmitancji.

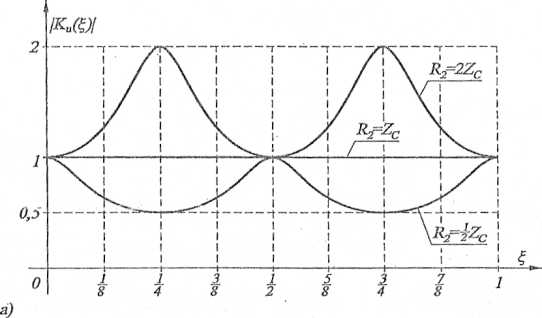
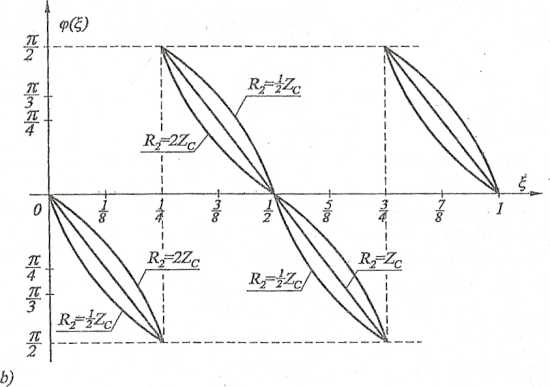
Rys. 14.16

Przykład 14.15

W obwodzie podanym na rys. 14.17 należy dobrać długość l₂ linii bezstratnej zwartej, tak by prąd I₂ na końcu linii bezstratnej o długości l_x był równy zeru. Dla tak dobranej wartości l₂ obliczyć prąd I_x i napięcie U* na początku linii l_x. Obydwie linie są to linie napowietrzne. Dane: e(f) = lOOy^sinorf V, f- 100 kHz, Z_x = (100 +j 128,7) L = = 0,5 mH, /j = 5 km, L₀₁ = 2-10'⁷ H/m, C₀₁ = 4 pF/m, = 10'tO”⁷ H/m, = 5 pF/m.

Zi

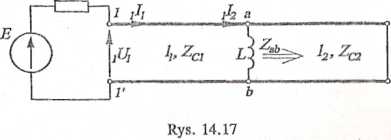
Rozwiązanie

Prąd na końcu linii /_t (_XI₂ ) jest równy zeru, jeżeli admitancja całkowita Y włączona na zaciski ab jest równa zeru. Ponieważ linia jest bezstratna, więc warunek ten sprowadza się do postaci

= o,

gdzie Z^ ■ jZ_c2tgfil₂. 1 1

Stąd---

<oL Z_c2tgpi₂

Ostatecznie

, czyli tg/SZj =    więc    = -arctg-^ + kir.

L = - Aarctg-^ +    » * = 0,1,2.....

² 2ir ⁶ Z_c2 2

W rozważanym przykładzie

/, = -0,29 + — = 1^1 km dla k = 1.

² * 2

Dla l₂ = 1,21 km linia o długości l_x jest nieobciążona, ponieważ zachodzi rezonans równoległy na końcu tej linii. Impedancja wejściowa z zacisków 11'

2-we H^; * Z we 10 ~    ~ j,

L_m 2ir

ctgi^/j = -j 128,7 n.

Prąd i napięcie na początku linii o długości l_x

= 1A, ₁U_l=Z_wtW-_lI_l = -jm,7V.

17

z„ +

At