skanuj0021 (141)

Z równowagi zaznaczonego węzła mamy

EP_ly = 0 K_ly+K_2y = 0 stąd    K_iy » - JC_aj, czyli K_{ ■ —K₂,

z symetrii wynika, że jK₄ = K₂. Oba warunki są zachowawo tylko w przypadku gdy K_t = K₂ = 0, co pozwala kolejno wyznaczyć siły w prętach metodą równoważenia węzłów.

a)    symetria struktury

b)    antysymetria obciążenia Wniosek: odpowiedź układu antysymetryczna (zakłócenia sił w pasie dolnym)

W tym schemacie analizę wygodnie zacząć od górnego węda kratownicy (przyjmując S(Q) = 0).

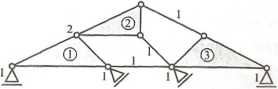
3.4. Kratownica o budowie złożonej

Przykład 20. Wykorzystując metody rozwiązywania kratownic wyznaczyć siły w prętach S_l9 D₂ kratownicy obciążonej jak na rysunku.

Schemat statyczny

gdzie:

w — liczba węzłów kratownicy w ■ 8, r — liczba reakcji (więzie podporowe) r = 4, p — liczba prętów p ■ 12,

12+4 = 2¹8.

Kryterium ilościowe jest zachowane! Kryterium to można także sprawdzić z warunku ilościowego e = 3t, po wcześniejszym jednoznacznym i prawidłowym podziale kratownicy na tarcze (pomoże to do innej analizy). W tym przypadku podział na tarcze pokazano poniżej, gdzie podano liczbę więzi elementarnych łączące tarcze między sobą. t — liczba tarcz (zawsze bez podstawowej) e = e_g+e_w

e_w — liczba więzi łączących tarcze między sobą, ale nie z podstawowi) — 1 + 1 + 1+2 = 5,

e_t — liczba więzi łączących tarcze z fundamentem (tarczą podstawową) e_x = l + l + l + l = 4

e = 4+5 = 9;    9 = 3¹3 — warunek zachowany (jak poprzednio).

Wobec zachowanego warunku ilościowego można wysnuć jedynie laki wniosek, że układ ten może był statycznie wyznaczalny {SW) jeśli będzie geometrycznie niezmienny I!

Oprócz zachowanego warunku ilościowego GN należy sprawdzić warun«4 jakościowy, stwierdzający prawidłową lokalizację więzi wewnętrznych |ak i zewnętrznych. Wykorzystywane są tutaj: twierdzenia o turc/ach, badanie wyznacznika układu globalnego lub zmodyfikowanego, metodu kinomalyu/nn z wykorzystaniem planu przesunięć, bądź metody specjalne np. metoda wymiany prętów Henneberga (najczęściej stosowana w kratownicacli złożonych).

Z analizy schematu statycznego kratownicy podzielonej na tarcze wynika, z.c nic mają bezpośredniego zastosowania twierdzenia o tarczach. Można by zaNtosować efektywną metodę badania wyznacznika (z punktu widzeniu matematyka) globalnego układu równań wypisując dwa równania równowugi dla każdego węzła (każdy węzeł to płaski zbieżny układ sił). Prowadzi to do ukludu równań o wymiarze 2w (niewiadome siły w prętach oraz reakcje). Można by analizować układ zmodyfikowany gdzie znane są już reakcje, któro hi| łatwe do wyznaczenia; w tym przypadku nie ma to jednak miojsa.

61

1

Przed przystąpieniem do rozwiązania zadania należy sprawdzić geometryczną niezmienność schematu statycznego.

Warunek konieczny geometrycznej niezmienności (GN) to warunek ilościowy (ale niewystarczający), który w przypadku płaskiego układu kratowego ma postać

p+r — 2w