skanuj0048 (18)

76

76

h

4

B. Cieślar
2 “ 4 ^1			(3)
6			(4)
•1 „	V'-2	_ Vr -3
l^rd	EdFd ’	^K * l*	(5)

Strona geometryczna

Strona fizyczna

Podstawiając równania (5) do (3) i (4), a następnie do (2) otrzymujemy:

V —0»⁵P-

^G E F '

1 ₊ EdLd

EM

Warunek równości naprężeń (1) przyjmie postać:

0,5P' p " E_dF_ri 2 ’

^t-ż^rż

a stąd:

P' = 1,41 P.

Tak więc, po wprowadzeniu dodatkowych podpór, siłę obciążającą można zwiększyć o 41%, bez wywołania dodatkowych naprężeń w słupie żeliwnym.

SsHi

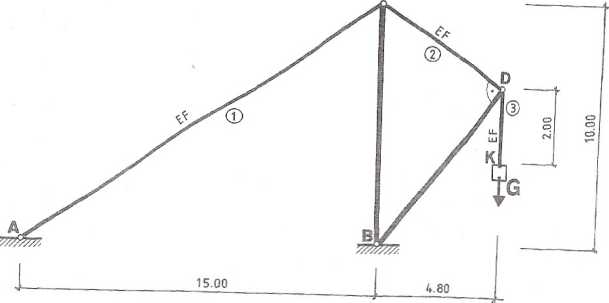
Ciężar Q jest zawieszony na linie żurawia, którego dwa maszty BC i BD

są podtrzymywane liną ACD (rys. 2.26.1). Określić dopuszczalną wartość ciężaru G, jeżeli pole przekroju liny F = 5 cm², a jej wytrzymałość obliczeniowa fd = 200 MPa. Następnie, zakładając dopuszczalną wartość ciężaru G oraz traktując maszty BC i BD jako idealnie sztywne, obliczyć, o ile obniży się punkt K zaczepienia ciężaru, jeśli E = 2-10⁵ MPa.

Rozwiązanie

Obliczenie wielkości pomocniczych (rys. 2.26.2)

AC = h = 18,03 m; sina = 0,5547;    cosa = 0,8321;

hi = ABsina = 8,321 m; sinji = 0,6; cos{3 = 0,8. Obliczenie sił w linach (rys. 2.26.2)

(D

(2)

(3)

£M^gd=0; G ^-S,^ =0; S^ 0,57690 £MS=0; g 4,8-S₂-8 = 0; S₂=0,6G;

£P_y = 0; S₃ =G.

C

Rys. 2.26.1

Obliczenie dopuszczalnej wartości siły G:

§L	0.5769G i.. F “	(4)
0>'|^LL II to*	0,6G , . F ^d’	(5)
s3	VI 0|u.	(6)

Rozwiązaniem nierówności (4), (5) i (6) będzie wartość wynikająca z nierówności (6), gdyż przy takim samym polu F największe naprężenie wystąpi w linie 3 (odcinek DK), tak więc:

fsfc GsPf_dF;

F-f_d ^5-ICT⁴ -200 = 0,1 MN;

a zatem:

G <0,1 MN = 100 kN.

Obliczenie obniżenia punktu zaczepienia ciężaru (K)

Przyjmując dopuszczalną wartość G = 0,1 MN, siły w linach będą równe:

Si = 0,05769 MN; S₂ = 0.06MN; S₃ = 0,1 MN.