skrypt027 (3)

52 Laboratorium Podstaw Elektrotechniki I

Sygnały:    u) u(t) - siu20t -I- 2cos(20t + i),

b) i(t) = eJ«‘

są sygnałami okresowymi. Okresy przedstawionych sygnałów wynoszą;

. >    i- _ 2 Jt _ n

'*    ~ia io *

sprawdzamy spełnienie warunku okresowości

0(1 + ~) = sin(20t +271) + 2cos(20t + ~ + 27t) =

- sin20t + 2cos(20t + ~) = u(t)

b) T= , i(t) = e-i²⁵ = cos25t + jsin25t

i{t + ?£-) = cos(25t + 27C) + j sin(25t + 271) = i(t)

Sygnały:	a)	u(t) = t,
	b)	u(t) - e'^101 ,
	c)	i(t) - cos h 3 Ot
		są sygnałami nieokresowymi

2.2. Wartość średnia sygnałów okresowych.

W zakresie teorii obwodów rozróżniamy dwie wartości średnie: wartość średnią calookresową i wartość średnią półokresową.

2.2.1.Wartość średnia całookresowa

Wartość średnią calookresową sygnału okresowego f(t) o okresie T określamy wzorem:

to + T

Fk. = —    (2.2)

tu

Początek granicy całkowania t₀ możemy wy'brać dowolnie. Sygnały okresowe których wartość średnia całookresowa jest równa zeru, nazywamy sygnałami pizemiennymi.

Wartość średnia półokresowa obliczona jest tylko dla sygnałów okresowych anty symetrycznych tzn. takich sygnałów, których wartości powtarzają się co pól okresu ale ze zmiennym znakiem. Funkcja antysymetryczna (domyślnie:    względem osi odciętych) spełnia warunek

2.2.2, Wartość średnia półokresowa

f(t +    = -f(t). Wartość średnią pólokresową sygnahi anty symetrycznego f'(t) o

okresie T, określamy wzorem:

n + T/2

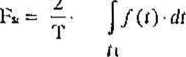
(23)

Wartość średnia określona wzorem (2.3) zależy w tym przypadku od wy boi u początku granicy całkowania t,. Jeżeli funkcja antysymetryczna ma dwie symetryczne połówki: dodatnią i ujemną, to czas t, we wzorze powinien stanowić początek dodatniej połówki sygnału.

Rozpatrzmy funkcję sinusoidalną f(t) = A sin(tot + ty)

Początki dodatnich połówek funkcji spełniają warunek:

tót = ty 2k7l (k=l,2,...)

czyli t = — (ty + 2k7l) Có

'lak więc za początek okresu całkowania możemy przyjąć t. = —

tu

Obliczamy wartość średnią pólokresową prądu sinusoidalnego:

i(t) = 1 sin(tót + ty)

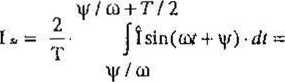
2    ] i    i{    i

— — I—l-cosfutf+u/n    =—(-cosTC + cosO) =2 —