skrypt5

6.3.1

^en.T

^rir,T

^rn.T \

Rys 6.3. Sekcja &{p_n+\ j) filtru

Cyfrowa rn.rracja anaptacyjna szeregów czasowych Stąd wniosek, że

k«+i >r=(k« >7 4-jarrt >_T p„+ij] < £„k„ >\< Cm-iK+i Wykorzystując tożsamość < <?„₊i|e_n+i >7= I otrzymujemy

I = < £_n\e_n >T< Cn41|*n+1 >T¹ [< *nl^e" >T + < C_n\zr_n >_T pn+\J +

+ < zr„\e_n >T p„+\.T+ < zr_n\zr_n >7 p** ,_<7] =

= < Knkn >T< Sfl+ lkn-fl >7' H ~ P«-f I ;7 “ Pn t I;7 + Pn+1 ij)

Mamy więc

^ £nkn ^7 ^ ^n+1 k« + t ^7 ^ ⁼ ( ^ Pn+ 1.7) ^ i ostatecznie

|e_n+| >7 — [ k„ >7 *H^jr« >7 Pnf 1:7 ](1 ""Pnf I;7)~

W analogiczny sposób możemy wyprowadzić zależność (6.48) Właściwość |p_nĄ.,_;7*| < I jest konsekwencją faktu. iż. współczynnik Schura wyraża się jako iloczyn skalamy unormowanych elementów \e_n >7 i |rr„ >7 przestrzeni 7/

n

/-ortogonalna realizacja filtru parametryzującego

Wykorzystując (6.10) i (6.11) w (6.47)-(6.48). i obliczając iloczyny skalanie

<    ar|e_n,.| >r=[< *\e_n >7 + < n\zr„ >7 p„₊i_;r ](I -pl+\ j)~ł    (6.50)

oraz

<    arkn+i >r= [ < rr\e„ >rPn+i.r+ < *\zr_n >r ](1 -p*+i.r)~*    (6.51)

otrzymujemy

*n+ l;7 = kn;7 +^r»»;r-IP/>+l:r](> “pi+l-.r)(6.52) oraz

r_n+\ J = kn;7Pfi+l;r + ^r/i;7-l](l ~ Pn+l j)~^    (6 53)

_Adaptacyjna parametryzacja ortogonalna szeregów czasowych

Przepisując (6.52)-(6.53) w postaci macierzowej

[t;;;]-«»-.») te„]

gdzie

0(P»+I:t) = (' -P»+nr)~ł [p_llłlT^P"⁺‘^]    (655)

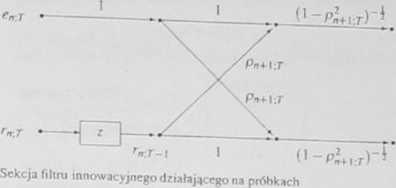
otrzymujemy ./-ortogonalną (spełniającą zależność Q{p_n*-\ j)J[p_n+\ j) = J) realizację sekcji filtru innowacyjnego, działającego na próbkach sygnałów. Zależności rckurencyjne (6.54)-(6.55) możemy przedstawić w postaci grafu przepływowego. pokazanego na rys. 6.2 i stanowiącego realizację pojedynczej sekcji filtru (dla n = 0... ,N - 1). Z zależności (6.54)-(6.55) wynika, że sekcję filtru z rys. 6 2 możemy schematycznie przedstawić w postaci z rys 6.3.

Jeśli zdefiniować

<w 4    [J J] = 0-P„²+l;,)-i [^_+1T    [J,°]    (6.56)

^en+\ T

^rn+\.T

140

Kitli nas

limu

141

Cyfrowa filtracja aoaptacyjna szeregów czasowych

tn-.T

tnW.T

U.T

Gi+I;r

RYS. 64 Sekcja ;7 filtru

to sekcję tę możemy schematycznie przedstawić na rys 6 4. Wówczas zależność rekurcncyjna (6.54) przyjmuje postać

*n+l;7

^rfi+I;7

= ft

>1+1:7

(6.57)

Z (6.57) wynika natychmiast realizacja kaskadowa (dla n = 0.. .N I) filtru innowacyjnego (parametryzującego), działającego na próbkach obserwowanego sygnału. W tym celu jest jedynie wymagane określenie jego inicjalizucji. Sta nowi ją element

ko >r= |eo >r< £o|eo >7 ^		(6.58)
W celu jego wyznaczenia przypomnijmy, żc
l®0 >r= |y >r = L>*o • • -yr]' skąd wniosek, że <*o|£a>j.=<		(659)
	A = Gf	(6.60)
Zatem
ko >7= |y >7 af^1 = [— ... — [crr G,\	II 'k' o	(6.61)
gdzie
a yt y» = — Gr		(6.62)
oznacza unormowaną próbkę sygnału obserwowanego (czyli próbkę sygnału standaryzowanego) Biorąc pod uwagę, żc - zgodnie z (6.45)-(6.46) -
ko >7“ ko >7		(6.63)

Aoaptacyjna parametryzacja ortogonalna szehegów czasowych

otrzymujemy ostatecznie

*0:7 = ^r0:T = Y7 = —

g_t

(664)

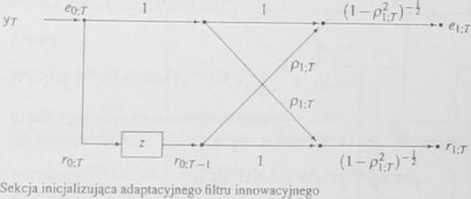
Wynika stąd sekcja inicjalizująca filtru, pokazana na rys. 6.5 lub - zgodnie z rys. 6.4 - sekcja z rys. 6.6. Realizacja kaskadowa filtru rzędu N przyjmuje więc postać pokazaną na rys. 6 7 Zauważmy, że z (6.57) dla n = 0,...,/V- I wynika, iż

(6.65)

y 7

7	0|;7
7

*1:7

rur

Rys. 6 6 Sekcja inicjalizująca 0\ j

y 7

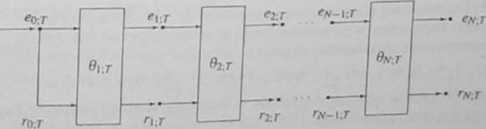
RYS. 6.7. Realizacja kaskadowa filtru innowacyjnego

143

142