str (71)

i

einsteinu

emulsions. The benzc&i^M high structural viscosit trations there is a kina

EQUA TION

outer cylinder, below which the emulsion does ^the flow at all. In tlie \vater/benzene emulsions at hu speeds there is a change in the form of the yiscosiS yelocity curve, which he claims marks the chanjjl from a solid to a liąuid type of friction. The difficulty lies in the fact that, in the case of an emulsion, assumptions cannot be madę about the incompressibility of the dispersed particles. In the case of a suspension, making the simplest assump-tions (a suspension of rigid spheres in a viscous hquid), Einstein arrives at an eąuation relating the viscosity of the suspension |g to that of the pure solvent g as follows

where <j> is the aggregate volume of spheres per unit vołume of suspension. This only holds in ptactice under conditions of extreme dilution. It should be noted that only the aggregate volume, and not the diameter of the particles, comes into the llpation. Baucelin finds fair agreement with this eąuation for gamboge suspensions:    Odeń also gets fair

agreement with sulphur-sols at Iow doncentrations. If one assumes hydration, a figurę for the increase in <f> can be obtained, which will give fait agreement over a considerably wider rangę. At really high concentrations the particles affect each other, and the whole treatment breaks down.

For emulsions, Taylor has modified the Einstein eąuation as follows

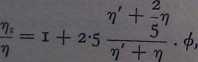
9 § _the yiscosity of the diapemed plisie, 'iifinmes inlinitc, this reducos to ICmsteins

emulsions investigated by them which are non-Newtonian fluids, they find in most cases, that

where is taken from the asymptote at high rates of shear, and a and § are constants. For long chain polymers, Staudinger gives a formula

I - i = K_mMc, V

where M = the molecular weight, and K_m = a, basie constant, and c the concentration. Houwink dis-cusses a later modification of this

= 2-5 V„c„,

where V₀ = a yoluminosity constant, and C„ = the volume concentration of the dissolved substance in a dry State. The yoluminosity, which is partly a measure of the degree of hydration, is partially dissipated in flow. Houwink also discusses a number of morę complex formulse.

Eirich and Goldschmidt have studied the flow of Suspeńsions of glass spheres. A modińed Einstein formula holds in the Couette apparatus where ^ < 6 per ceni, but viscosities are lower in the capillary tubę apparatus.

Golloidal particles are charged, and the charge