str071 (2)

mu.¹¹ i ¹ 'i/yhllżnnu w. ii li i zyrtnlków odi I "luli l|i |> V III.....ich '.nltllllÓW ()l ’! J om/ leli ulu link

mu.¹¹ i ¹ 'i/yhllżnnu w. ii li i zyrtnlków odi I "luli l|i |> V III.....ich '.nltllllÓW ()l ’! J om/ leli ulu link

Działająca silu	Mn|. nymalnn pizyśpInn/DiiIn |m/n |	Maksymalny otoki zakłócenia po 1 li |in|
/• grawitacja Zloml	O.ÓB-U)^1	-
/, grawitacja Księżyca	0,8 ■ 10"	40
i , grawitacja Słońca	3.0-10"	2
/clftnlonio światła słonecznego	1.0-10'	0.6
/ anomalie siły ciężkości	1.0-10-^8	0.06
Inno	1.0-10^8	0.06

0.2, Niezakłócony ruch SSZ 0.2.1. Siła ciężkości

Ruch sztucznego satelity Ziemi względem ciała centralnego, w najbardziej uproszczonej formie, jest typowym ruchem po okręgu, znanym z kursu fizyki podstawowej. Jego istotąjest /miana kierunku wektora prędkości liniowej, skutkująca występowaniem przyśpieszenia i siły dośrodkowej. Uwzględniając masę satelity siłę dośrodkową działającą na niego opiszemy folncjn

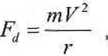
(6.1)

gd/le:

ni masa satelity,

I prędkość liniowa satelity w ruchu po orbicie kołowej, r promień orbity.

W rozważanym ruchu po okręgu, siłą dośrodkowąjest siła przyciągania ziemskiego wynikająca z prawa powszechnego ciążenia postaci

F,=G

Mm

(6.2)

gdzie:

(i ulata grawitacyjna równa 6.672• 10~¹¹m³kg'¹s~² ,

M masa Ziemi wynosząca ok. 5.97-10²⁴kg .

Inn prosty model zakłada szereg uproszczeń, do których należą: satelita oraz Ziemia, są punktami materialnymi o masach skupionych w jednym punkcie. Przyjmuje się, że pominięto w nim oddziaływanie grawitacyjne innych ciał. Zależność (6.2) często prezentowana jest w formie wektorowej. Aby przekształcić ją do tej postaci, należy obrać wektor r (rys. 6.2) — łączący oba ciała (Ziemię i satelitę) oraz wartość siły pomnożyć przez wektor jednostkowy - y .

orbita ^

Ziemia

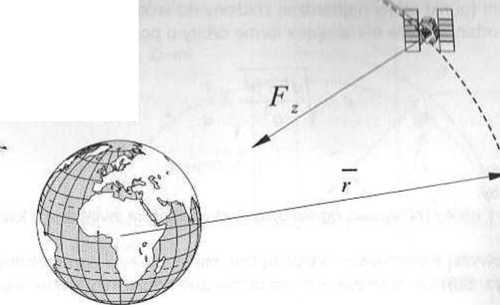
Rys. 6.2. Oddziaływanie sity centralnej na poruszającego się satelitę,

Otrzymamy w ten sposób wektorowy opis siły działającej na poruszającego się satelitę pi mim

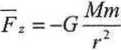
r

r

(6 :i

Zapis powyższy informuje, że wektor siły grawitacyjnej leży na prostej przechod/ącni pi/", środek Ziemi i satelitę oraz wskazuje również jego zwrot. Aby satelita utrzymał kołow;| Iriijtik torię swego ruchu, powinien posiadać określoną prędkość liniową będącą w ścisłym związki z promieniem orbity, jak również masą satelity. Zachwianie tej swoistej proporcji skutkuje zmlnt» kształtu orbity, co w konsekwencji doprowadzić może do „upadku” satelity na Ziemię lub |t>||< „ucieczki” w kosmos. Z tego względu satelity wyposażane sąw silniki korekcyjne, dzięki któiyn możliwym jest bieżąca korekta trajektorii.

6.2.2. Elementy orbity

Współrzędne poruszającego się po orbicie wokółziemskiej satelity można jednoznm:/ nie opisać w funkcji czasu przy pomocy pewnych parametrów zwanych elementami orbity W przypadku orbity eliptycznej, z którą mamy do czynienia w GPS, są nimi:

>    a - duża półoś orbity elipsy, określająca rozmiary jej oraz będąca w ścisłym związki z okresem obiegu satelity wokół ciała centralnego,

>    i - inklinacja orbity jest kątem nachylenia płaszczyzny orbity do płaszczyzny ekliptyk (równika). Dla systemu GPS wartość inklinacji wynosi 55°. Inklinacja jest kątem dwuśclen nym. Jeżeli 0< i <90 to satelita porusza się po tzw. orbicie prostej, a dla 90< i <1t)( mamy do czynienia z orbitą wsteczną.

>    Q - długość węzła wstępującego orbity odpowiada długości ekliptycznej punktu przeclę cia orbity z płaszczyzną ekliptyki. Odniesiona ona jest do zmiany szerokości ekliptyczne z ujemnej na dodatnią.

14