Str083

162    3. I.ićJiby pierwftte i rozkład nn czynniki

kongrucncji, tzo. jeśli będziemy podnosili b do potęgi (n — l)/2, (n — l)/4, .._#ł (n - l)/2^ł (gdzie / - (n - l)/2* jest liczbą nieparzystą), to pierwszą resztą mo-duło n, różną od 1, jaką otrzymamy, musi być -1, jeśli n jest liczbą pierwszą, bo i 1 są jedynymi pierwiastkami kwadratowymi z I modulo liczba pierwsza. W rzeczywistości wykonujemy obliczenia w przeciwnym kierunku. Przyjmujemy najpierw n - 1 =2*/, gdzie / jest nieparzyste, następnie obliczamy b^l mod n, następnie (jeśli b' nic przystaje do 1 modulo n) podnosimy wynik do kwadratu, by otrzymać b^lx mod n, znów podnosimy do kwadratu, by otrzymać 6^2łf mod n itd., tak długo, aż po raz pierwszy otrzymamy resztę 1 modulo n\ wtedy w poprzednim kroku przed otrzymaniem 1 musimy otrzymać — 1 lub - w przeciwnym razie - przekonamy się, że liczba n jest złożona.

Definicja. Niech n będzie nieparzystą liczbą złożoną i niech n — 1 = 2‘t, gdzie liczba / jest nieparzysta. Niech 6e(Z/nZ)*. Jeśli liczby n i b spełniają warunek

b^l = 1 (mod ń) lub

istnieje liczba r, 0 < r < s. taka, że b^2r{ = — 1 (mod n),    (3)

to liczbę n nazywamy liczbą silnie pseudopierwszą przy podstawie b.

Twierdzenie 5.1.5. Jeśli n = 3 (mod 4), to liczba n jest silnie pseudopierwszą przy podstawie b wtedy i tylko wtedy, gdy jest liczbą pseudopierwszą Eulera przy podstawie b.

Dowód. Ponieważ w tym przypadku s = 1 i / = (n — l)/2, to widzimy, że liczba n jest silnie pseudopierwszą przy podstawie b wtedy i tylko wtedy, gdy b^{*~ D^/2 = ±1 (mod n). Jeśli n jest liczbą pseudopierwszą Eulera, to ta kon-gruencja zachodzi z definicji. Na odwrót, przypuśćmy, że = ± 1. Musi

my pokazać, że +1 po prawej stronie jest równe . Ale dla n = 3 (mod 4)

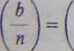
b • (6²)⁽"-³>'⁴

n

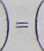
£(«-1)/2

n

= ó<"-^1)/2 (mod ń),

czego należało dowieść.

Następne dwa twierdzenia są trochę trudniejsze do udowodnienia.

Twierdzenie 5.1.6. Jeśli n jest liczbą silnie pseudopierwszą przy podstawie b, to jest liczbą pseudopierwszą Eulera przy podstawie b.

Twierdzenie 5.1.7. Jeśli n jest nieparzystą liczbą złożoną, to n jest liczbą silnie pseudopierwszą przy podstawie b dla co najwyżej 25% wszystkich takich podstaw b, że 0 < b <n.

jj_wflga. Twicrdzenic odwrotne do twierdzenia 5.1.6 nic jest na ogół prawdziwe, o czym przekonamy się w ćwiczeniach.

Zanim udowodnimy powyższe dwa twierdzenia, opiszemy test pierwszo-g_ci Millera-Rabina. Przypuśćmy, że chcemy stwierdzić, czy duża nieparzysta liczba naturalna jest liczbą pierwszą czy złożoną. Piszemy n- 1 = 2'f, gdzie liczba t jest nieparzysta, i wybieramy losową liczbę b, 0 < b < n. Najpierw obliczamy b^l mod n. Jeśli otrzymamy ± 1, to stwierdzamy, że liczba n pnc$7k pomyślnie przez test (3) dla naszej szczególnej podstawy b i wybieramy następną losową podstawę b. W przeciwnym razie podnosimy do kwadratu b^x modulo n, potem otrzymany wynik podnosimy do kwadratu modulo n itd., tak długo, aż otrzymamy -1. Jeśli otrzymamy -1, to liczba n pomyślnie przeszła test. Jeżeli jednakże nigdy nie otrzymamy -1, tzn. jeśli osiągniemy h?*' = 1 (mod ń), podczas gdy b^v £ -1 (mod n), to liczba n nie przeszła pomyślnie testu i wiemy, że jest ona złożona. Jeśli liczba n przejdzie pomyślnie test (3) dla wszystkich losowo wybranych b - przypuśćmy, że próbujemy k różnych podstaw b — to wiemy na podstawie twierdzenia 5.1.7, że n ma jedną szansę na 4* na to, by być liczbą złożoną. Jest tak dlatego, że jeśli n jest złożona, to co najwyżej 1/4 podstaw 0 < b < n spełnia (3). Zauważmy, że jest to trochę lepiej niż w przypadku testu Solovaya-Strassena, gdzie analogiczne oszacowanie daje jedną szansę na 2* (ponieważ istnieją złożone liczby n, które są liczbami pseu-dopierwszymi Eulera dla połowy wszystkich podstaw 0 < b < n, o czym przekonamy się w ćwiczeniach).

Przejdziemy teraz do dowodów twierdzeń 5.1.6 i 5.1.7.

Dowód twierdzenia 5.1.6. Dane są n i b spełniające warunek (3). Musimy pokazać, że spełniają one kongruencję (2). Niech n - 1 = 2*/, gdzie liczba t jest nieparzysta.

Przypadek (i). Przypuśćmy najpierw, że b^l s 1 (mod n). Wtedy lewa

strona (2) oczywiście wynosi 1. Musimy pokazać, że =1. Ale

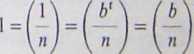
my pokazać, że wtedy

. Ponieważ liczba / jest nieparzysta, to

nnćrnw nastannie 7ft A(ⁿ~0/2 = — 1 Imt

= 1.

Przypadek (ii). Przypuśćmy następnie, że ó⁽ⁿ~^1,/2 = -1 (mod n). Musi-

1. Niech p będzie dowolnym dzielnikiem

pierwszym liczby n. Zapiszmy1 w postacip - 1 = 2* gdzie liczba r'jest nieparzysta, i udowodnijmy następujące stwierdzenie:

Stwierdzenie. Zachodzi nierówność s' > s oraz równość

b

P

-1, jeżeli s' = j, 1, jeżeli s¹ > s.