Image009 (50)

Jerzy Chromieć, Stanisław Lindner

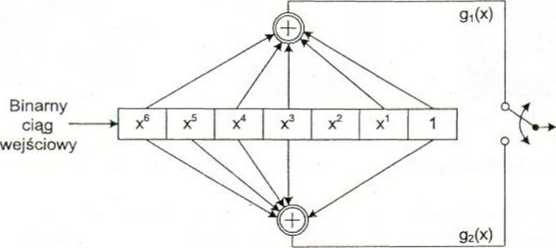
g,(x) = x⁶+x⁴+ x³+x+l ,    (_gl)=(1011011|

g₂(x) = x⁴+xⁱ+x⁴+x³+l ,    jg₂)={1111001j

W zapisie dziesiętnym g, = 91, g₂ = 121.

Ciąg

kodowy

Rys. 1.11. Schemat kodera splotowego (2,1,7)

Istotnym parametrem kodu splotowego jest sprawność kodowania R. Informuje ona o tym, ile bitów wyjściowych z kodera przypada na pojedynczą sekwencję bitów wejściowych kodera. W przybliżeniu R = k/ n. Sprawność kodowania kodera z rys. 1.11 w^rnosi R = 1 / 2. Kod splotowy charakteryzowany jest też przez odległość swobodną d_f , będącą najmniejszą odległością Hamminga między dwoma dowolnymi sekwencjami o tej samej długości otrzymywanymi z wyjścia kodera. Im większe d_(ree tym możliwości korekcyjne kodu są większe.

Poniżej, w tabeli 1.1. przedstawiono maksymalne osiągalne odległości swobodne dla kodów splotowych systematycznych i niesystematycznych o sprawności kodowania R=l/2 dla różnych długości wymuszonych K. Na ogół preferuje się stosowanie kodów splotow7ch niesystematycznych gdyż zapewmiają one lepsze zdolności korekcyjne. W kodach niesystematycznych, w przeciwieństwie do kodów' systematycznych nie da się jednak wyróżnić części informacyjnej i nadmiarowej.

Tabela 1.1. Maksymalne osiągalne odległości swotx>dne dla kodów splotowych o sprawności R-l/2

Długość wymuszona K	Odległość swobodna
	Kod systematyczny	Kod niesystematyczny
2	3	3
3	4	5
4	4	6
5	5	7
6	6	8
7	6	10
8	7	10

Kod o odległości swobodnej d_fm może skorygować t błędów wtedy i tylko wtedy gdy d_f jest większa od 2ł. Przykładowo kod niesystematyczny o K = 5 i odległości swobodnej d,_{r r}= 7, w obrębie podciągu o długości (4 +5) K = 20±25 bitów jest w stanie skorygować

t = —^—ł - 3 błędy, jeśli są one niezależne statystycznie.

2

Istnieją sytuacje, kiedy sprawność kodowania rzędu R-l/n jest nieodpowiednia a preferowana jest sprawność R=k/n, np. ze względu na niską stopę błędów binarnych w kanale. Wówczas istnieją dwie możliwości postępowania: budowa kodera o k rejestrach przesuwnych, który każdorazowo na wejście przyjmuje k bitów informacyjnych i generuje n bitów wyjściowych albo zastosowanie tzw. kodu RCPC (Ratę Compatibile Punctured Cowolutional Codę).

W pierwszym przypadku struktura kodera ulegnie znacznej komplikacji, natomiast drugie podejście polega na wykluczaniu (puncturing) niektórych bitów pierwotnego ciągu kodowego. Punktem wyjścia tej metody postępowania jest kod o sprawności R=l/2 uzupełniony o łatwo modyfikowalną tablicę wykluczeń. Kod RCPC zapewnia wykluczanie okresowo niektórych bitów' zgodnie z tablicą wykluczeń, w której znajdują się zera i jedynki. Tablica wykluczeń dla ustalonego R określa, z której gałęzi kodera bity w każdej sekwencji par bitów wyjściowych kodera zostaną wykluczone. Symbol jedynki w takiej tablicy oznacza, że dany bit wyjściowy kodera zostaje przekazany na wyjście, zero oznacza, że zostaje wykluczony.

Tabela 1.2. Przykładowa tablica wykluczeń dla K=7.

Sprawność kodu R	Tablica wykluczeń	Odległość swobodna d(m
1/2	1	10
	1
2/3	10	6
	11
3/4	101	5
	110
5/6	10101	4
	11010
7/8	1000101	3
	1111010

1.4. TECHNIKI TRANSMISJI

Wybór odpowiednich technik transmisji wiąże się z wyborem rodzaju zwielokrotnienia dostępu do kanału; FDM, TDM, CDM i SDM lub ich odmiany EDMA, TOMA, CDMA, SDMA oraz ze sposobem wykorzystania pasma kanału radiowego. Priorytetem może być bowiem uzyskanie maksymalnej efektywności widmowej transmisji £ (spectrał

21