skanuj0162

122

drgania osiągają, maksymalną amplitudę 2A.

122

Natomiast w punktach zwanych węzłami drgania nie występują. Ich współrzędne dane są wzorem:

1.3. Prędkość fali akustycznej

Fale rozchodzące się w powietrzu, które docierając do naszego ucha wywo-11 ij ą wrażenie dźwięku mają częstotliwość/z przedziału od 16 do 20 000 Hz.

Prędkość propagacji fali zależy od mechanicznych własności ośrodka, kozchodząca się w gazie fala dźwiękowa jest falą podłużną polegającą na przemieszczaniu się jego zagęszczeń i rozrzedzeń (rys.5). Ze względu na dużą prędkość rozchodzenia się fali możemy przyjąć, że mamy do czynienia z procesami adiabatycznymi, a wówczas otrzymujemy wzór na jej prędkość w postaci:

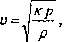
.''.'Izie K-Cp/cy jest stosunkiem ciepła właściwego przy stałym ciśnieniu do > icpła właściwego przy stałej objętości, p - ciśnieniem, p gęstością gazu. Uwzględniając, że zależność gęstości gazu od temperatury dana jest wyrażeniem²:

/>(0 = />₀/(l + aO.

pil/.ie p₀ jest gęstością w t = 0°C, a- 1/273,15 °C~^{1 2} współczynnikiem rozsze-walności objętościowej gazu, t temperaturą w skali Celsjusza, otrzymujemy:

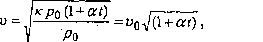
(7)

gdzie i>„ to prędkość rozchodzenia się dźwięku w powietrzu w temperaturze 0°C, bez względu na jego ciśnienie. W suchym powietrzu u₀= 331,5 m/s.

2. Metoda pomiaru

Akustyczne fale stojące można wzbudzić w słupach powietrza. Jeśli jeden koniec rury jest zamknięty, to fale wzbudzane u wylotu rury rozchodzą się w powietrzu i odbijająna jej końcu. Fala stojąca powstaje w wyniku superpozycji fal padających i odbitych. Jeśli długość półotwartej rury spełnia warunek:

/ =—-⁺¹— , gdzie n = 0,1,2,...    (8)

4

to na zamkniętym końcu rury powstaje węzeł, a na końcu otwartym strzałka fali stojącej (rys. 6). Amplituda drgań u wylotu rury osiąga maksymalną wartość i jednocześnie obserwuje się silne wzmocnienie dźwięku.

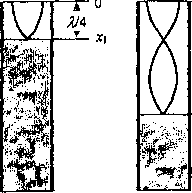
Rys.6. Fale stojące w rurze jednostronnie otwartej

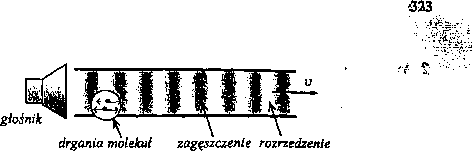
Rys.5. Fala dźwiękowa rozchodząca się w powietrzu (mechaniczna fala podłużna). Zaznaczono kierunki drgań molekuł gazu oraz kierunek propagacji fali

Pomiar długości słupa powietrza, w którym powstaje fala stojąca, jeśli znamy częstotliwość / źródła wymuszającego drgania, pozwala wyznaczyć ze wzoru (8) długość fali A oraz prędkość dźwięku v = Af.

l )la gazu w temperaturze T (w skali Kelwina), objętości V i pod ciśnieniem p mamy

1

^    ^T = — — (1 + at), gdzie p_a, V₀ to odpowiednio ciśnienie i objętość w 0°C

/' m m Tq m

2

² 'yb w To = 273,15 K), m - masa gazu, t - temperatura w °C, a= 1/273,15 °C.