transformata fouriera opis właściwości okienka v2 2

<-od O_3*AA=3.0    _do 3-> |

<-od 0    2*AA=2.0    do 2->    Amplituda

<-od0 AA=1.0 dol-ft<-odO AA=1.0 do !->||<^oćl 0 AA=1.0 do 1->|

Def: punkt to układ współrzędnych skończonych wymiarów

którego rozdzielczość to suma rozdzielczości wszystkich punktów czyli pi()

a jednostka_:to a czyli: x=a*pi(),y=a*pi() gdzie znak określa spin,biegun

^a — =—    > amplituda=a*pi()+a*pi()=2*a*pi()

a*pi() a

Obiektowość typu:

rozdzielczość punktu.Y=Yl rozdzielczość okienka.amplituda = aa=i.o rozdzielczość wykresu.aplituda = k*AA

rozdzielczość punktu.X=Xl a=i/n rozdzielczość okienka.czas = At= ^•^^nek.w.i_fo[si

gdy N=f gdy N=f

N

sin(x)

rozdzielczość wykresu.czas=AT= ^N

N

gdy N=f

	X	© rewertynPL
	w
<-od 0.0 At=!!^ęiv_i.oui do At-> M		n n H5.:<lene.:.w.i.0ls| rlr» A+-> M	<-od 0.0 At= "^5--^<lenev-"-uw do At-> -H-
<-od 0.0 At=2* —		^c,ene’^:wJ'^0tsl do 2*At ->

3

C

3

a

'O

'W

O

N

O

N

“O

N

O

rozdzielczość punktu

/

CZaS max = ls*m

<- od 0.0	N _ ile.ckienek.w.l.Olsl AT— -ilHZj	do AT=l[s] ->
	N ^N

+■

& =l[s]

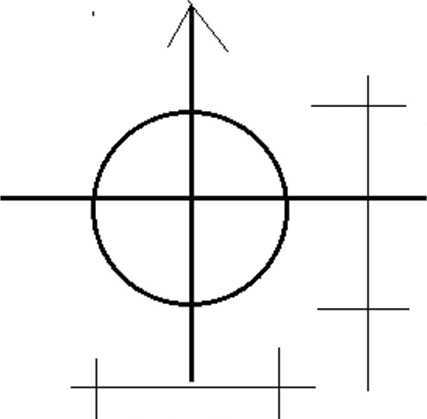
Zapis wzoru fouriera pomaga obliczyć

obrót każdego punktu o znanej rozdzielczości A czyli spin

h(x) = g(x) * sin( ±co +    ± j sin( co)

wynik macierzy:

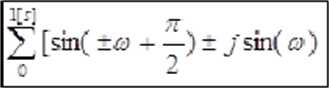
/(*>) = z *[^sin(    J'sin(>)]

o    2

wynik funkcji to zsumowane wszystkich punktów które nie mają punktu odbitego lustrzanie,o zadanej rozdzielczości splotu

wynikiem macierzy bez sumowania punktów jest wykres funkcji lustrzanych z uwzględnionym obrotem każdego punktu,spin

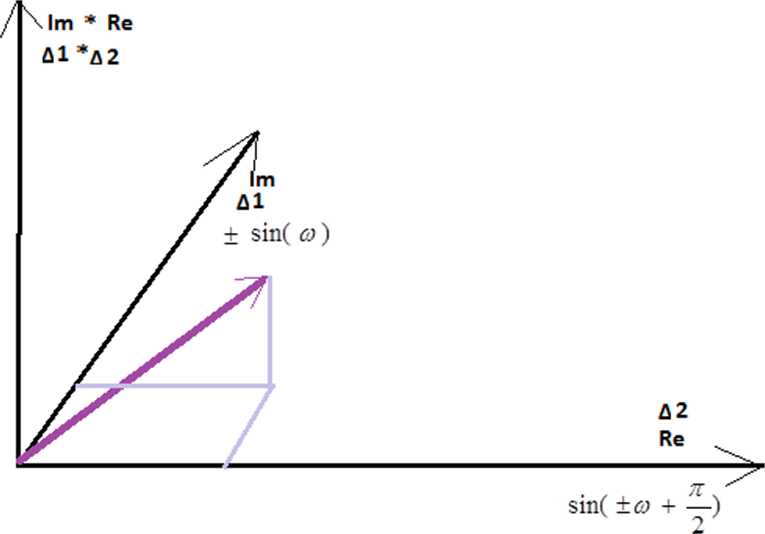
pole wszystkich możliwych punktów w okienku liczb rzeczywistych ?= pole koła liczb zespolonych