54564 MaszynaW 30

62 4. Program ćwiczeń

Mając przygotowane wszystkie potrzebne rozkazy, możemy przystąpić do projektowania programu liczącego odpowiednią liczbę Fibonacciego. Zauważmy, że podana definicja liczby Fibonacciego jest typową definicją rekurencyjną, gdzie wartość następnej liczby w ciągu zależy od wartości dwu liczb bezpośrednio ją poprzedzających. Sam program należy zatem podzielić na dwie części: program główny i procedurę Fib liczącą kolejną liczbę (informacja

0    tym, która to ma być liczba, będzie przekazana jako parametr lej procedury umieszczony w akumulatorze, tam też będzie zwracany wynik). Zacznijmy od programu głównego. Będzie on składał się zaledwie z kilku rozkazów:

-    pobrania odpowiedniej liczby do akumulatora,

-    wywołania procedury Fib,

-    przesłania wyniku wykonania tej procedury do komórki pamięci oznaczonej etykietą Wynik.

Dużo bardziej złożona będzie procedura Fib. Nim podamy jej opis w języku asemblera, spróbujmy najpierw zapisać ją w języku wyższego poziomu, np. w Pascalu. Z założeń wynika, że Fib< 0 ) = 0 i Fib( 1 ) = 1. A dla n > 1:

Fib( n ) = Fib( n - 1 ) + Fib{ n - 2 ).

Zapisana w Pascalu funkcja licząca kolejne liczby Fibonacciego powinna więc wyglądać następująco:

funetion Fibl n : integer |: integer; begln

If ( n = 0 ) or I n * 1 ) then Fib : * n

elsa

Fib : = Fib| n • 1 J + Fibl n - 2 ł

and;

Podobnie będzie wyglądać odpowiednia procedura w języku asemblera. Parametr n jest przekazany w rejestrze Ak. Tam też powinien znaleźć się wynik. Na początku należy sprawdzić, czy n jest równe zero lub jeden. Jeśli tak, to wynikiem procedury będzie wartość parametru n i tę wartość należy zwrócić. Badanie, czy n = 0, można wykonać za pomocą rozkazu SOZ testującego zero w akumulatorze i wykonującego w takim przypadku skok. Nieco trudniejsze jest zbadanie warunku n = 1. Można również wykorzystać rozkaz SOZ. należy jednak wcześniej zdekrementować zawartość akumulatora (rozkazem ODE Stl)

1    w przypadku stwierdzenia równości pamiętać o przywróceniu starej zawartości akumulatora przed powrotem z procedury. Z bardziej złożonym problemem mamy do czynienia, gdy n > 1 (odpowiada to frazie ehe w rozwiązaniu w Pascalu). W tym przypadku, by obliczyć wartość n-tej liczby w ciągu Fibonacciego, należy, korzystając z tejże procedury, obliczyć dwie poprzednie liczby i dodać je do siebie. Zauważmy przy tym, że ani wartości parametru n, ani sumy częściowej nie można przechowywać w jakiejś z góry ustalonej komórce pamięci. Jedynym możliwym rozwiązaniem jest przechowywanie tych wartości na stosie (stąd

tak

start

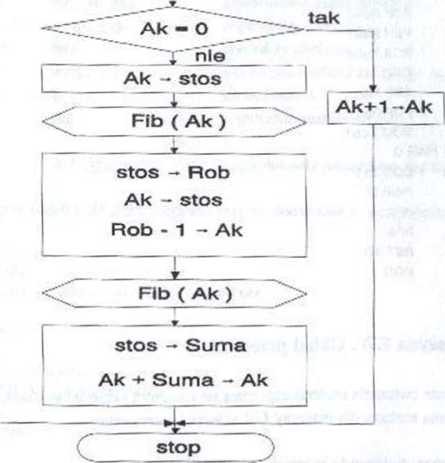
Rys. 4.2. Schemat blokowy programu obliczającego liczby Fibonacciego

wynikła konieczność przygotowania rozkazów PSH i POP). Pełne rozwiązanie, w postaci schematu blokowego, przedstawiono na rysunku (rys. 4.2.), a poniżej zamieszczono treść programu w języku asemblera.

{ Program główny } start:    POB Liczba

SDP Fib LAD Wynik Stop:    SOB Stop

Liczba: RST 4D Wynik: RPA