60296 P3200052

Rysunek 4.9A Wyniki grupowania    Rysunek 4.9B. Wyniki grupowania

(z obiektami nietypowymi)    (bez obiektów nietypowych)

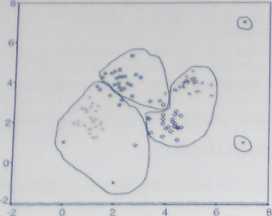
Powyższy zbiór obiektów został otrzymany przez wygenerowanie 4 populacji o różnych rozkładach normalnych i dodanie 4 obiektów nietypowych. Procedury analizy skupień bezbłędnie identyfikują grupy, jeżeli przyjmiemy b= 8 (z obiektami nietypowymi) i k=A (bez obiektów nietypowych). Jeżeli przyjmiemy k-3 lub k=5, otrzymujemy nieprawidłowy podział. Ten przykład pokazuje też, jak obecność obiektów nietypowych drastycznie zmienia wyniki grupowania.

Ustalenie właściwej liczby skupień jest jednym z najtrudniejszych i najważniejszych problemów przy przeprowadzaniu grupowania obiektów. Problem ten, chociaż rozważany w wielu publikacjach (np. [Everitt 1980], [Hartigan 1985], [Milligan, Cooper, 1985], [Jain, Moreau. 1987], [Hardy, 1996]) i często podejmowany w praktyce, nie został do tej pory w pełni rozwiązany. W wielu przypadkach badane zbiory mają pewne naturalne tendencje do grupowania się w jednorodne klasy, co znacznie ułatwia ich anaii v Jeżeli obiekty w wyodrębnionych klasach są do siebie podobne, a jednocześnie u ,'ią wyraźne różnice między klasami, wtedy zidentyfikowanie tych klas nie jest zad trudnym. Często jednak mamy do czynienia z sytuacją, gdy skupianie się obiektów w y.dnorodne klasy nic jest wyraźne.

Liczbę skupień wybiera się na podstawie przesłanek merytorycznych albo szacuje się je metodami hierarchicznymi. Jedna z najprostszych polega na wielokrotnym przeprowadzaniu procedury grupowania, przyjmując kolejno k skupień z ustalonego przedziału: k < k < k . Wybór początkowego podziału jest równoważny ustaleniu początkowych

zalążków środków ciężkości, ponieważ:

- znając początkową przynależność obiektów do grup możemy obliczyć środki ciężkości

gruj - /.na rzą Następ

wania. jeżeli mniejs miar j distar

środk

J.C.B skupi Dlate rze Si jedni towa hic C CCC tych ares toda ka P nost zapt obst loso moi liczi mai nej

wp

Wi_c

pow

ślad

146