Temat.
Wyznaczenie sztywności belki zginanej (moduł Younga E, moment bezwładności Ix)
Cel ćwiczenia.
Celem ćwiczenia jest wyznaczenie modułu Younga poprzez pomiar ugięć belki zginanej różnymi metodami. Zapoznanie się z metodami pomiarów oraz z metodami pomiarów oraz identyfikacją schematów statycznych, błędów pomiaru itd...
Metody stosowane do pomiarów przemieszczeń:
duże obiekty - metody geodezyjne (niwelacja)
elementy konstrukcyjne i modele - czujniki przemieszczeń ( czujniki zegarowe, redukcyjne i tensometry)
płyty - metoda interferencji, metody graficzne
metody stereo fotogrametryczne - fotografia
Schemat stanowiska badawczego.
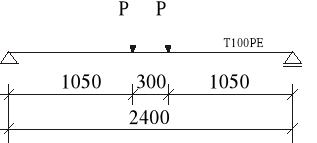
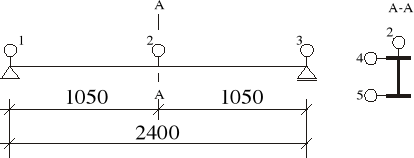
Rozpatrujemy belkę swobodnie podpartą o rozstawie podpór 240,0 cm, obciążoną dwiema siłami skupionymi odległymi od siebie o 30,0 cm. Schemat przedstawiono na rysunku.
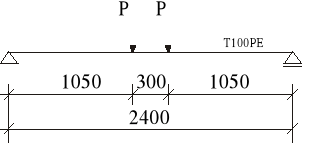
Rozmieszczenie przyrządów pomiarowych.
Na belce rozmieszczono pięć czujników zegarowych z których trzy mierzą ugięcia a dwa pozostałe wychylenie osi belki od pionu.
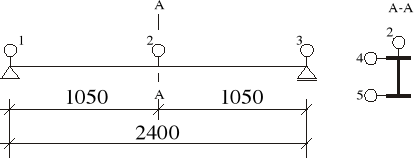
Przebieg ćwiczenia.
5.1. Pomiar długości belki L (odległość między osiami podpór)
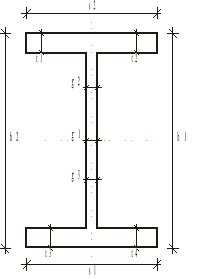
5.2. Pomiar wymiarów przekroju poprzecznego, odczytanie i obliczenie momentu bezwładności Ix.
5.3. Ustalenie współrzędnych przyłożenia siły oraz punktów pomiarowych.
5.4. Dla kilku wartości siły P zmierzyć ugięcie y`.
5.5. Wyniki zebrać w tabeli.
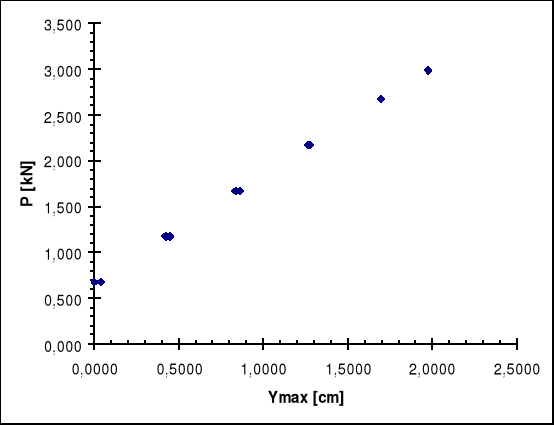
5.6. Sporządzić wykres y = f (P)
5.7. Zinterpretować wyniki.
Wyniki pomiarów i wyznaczenie poszukiwanych wartości.
Długość belki L = 2400 mm.
Tab. 1 Charakterystyka geometryczna przekroju.
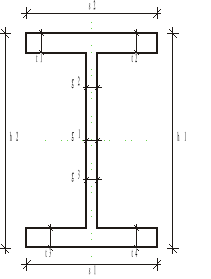
Pomiar |
t1 |
t2 |
t3 |
t4 |
g1 |
g2 |
g3 |
h1 |
h2 |
s1 |
s2 |
|||
1 |
6,0 |
5,7 |
6,4 |
5,7 |
4,6 |
4,7 |
4,7 |
101,6 |
101,0 |
53,2 |
53,9 |
|||
2 |
6,0 |
6,1 |
5,8 |
6,2 |
4,5 |
4,6 |
4,6 |
100,9 |
101,2 |
53,6 |
54,0 |
|||
3 |
5,9 |
5,5 |
5,6 |
5,8 |
4,6 |
4,6 |
4,8 |
101,0 |
101,5 |
53,4 |
54,0 |
|||
Wart. średnie |
5,97 |
5,77 |
5,93 |
5,90 |
4,57 |
4,63 |
4,70 |
101,17 |
101,23 |
53,40 |
53,97 |
|||
Wartości |
t |
g |
h |
s |
||||||||||
- pomierzone |
5,892 |
4,633 |
101,200 |
53,683 |
||||||||||
- normowe |
5,7 |
4,1 |
100,0 |
55,0 |
||||||||||
Ixp |
171,438 cm4 |
|||||||||||||
Ixno |
163,323 cm4 |
|||||||||||||
Ixn |
171,000 cm4 |
|||||||||||||
- moment bezwładności policzony na podstawie pomiarów zestawionych w tabeli. ![]()
moment bezwładności obliczony na podstawie wartości z tablic, normowych (tab. 1)
![]()
moment bezwładności odczytany z tablic
![]()
Średni moment bezwładności: 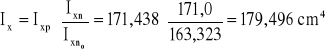
Tab.2 Tabela pomiarów zwichrzenia. Waga = 66,9 kG
Obciążenie |
Odczyt z czujników |
Zwichrzenie [cm] |
|
|
|
|||
kG |
kN |
czujnik 4 |
czujnik 5 |
górna półka |
dolna półka |
d[cm] |
Φ [10-3] |
Δ[cm10-4] |
66,9 |
656,289 |
4,300 |
4,880 |
0,000 |
0,000 |
0,000 |
0,00000 |
0,000 |
116,9 |
1146,789 |
4,425 |
4,925 |
0,125 |
0,045 |
0,080 |
0,80000 |
0,320 |
166,9 |
1637,289 |
4,520 |
4,980 |
0,220 |
0,100 |
0,120 |
1,20000 |
0,720 |
216,9 |
2127,789 |
4,665 |
5,025 |
0,365 |
0,145 |
0,220 |
2,20001 |
2,420 |
266,9 |
2618,289 |
4,820 |
5,095 |
0,520 |
0,215 |
0,305 |
3,05001 |
4,651 |
298,9 |
2932,209 |
4,950 |
5,140 |
0,650 |
0,260 |
0,390 |
3,90003 |
7,605 |
266,9 |
2618,289 |
4,840 |
5,080 |
0,540 |
0,200 |
0,340 |
3,40002 |
5,780 |
216,9 |
2127,789 |
4,710 |
5,015 |
0,410 |
0,135 |
0,275 |
2,75001 |
3,781 |
166,9 |
1637,289 |
4,550 |
4,960 |
0,250 |
0,080 |
0,170 |
1,70000 |
1,445 |
116,9 |
1146,789 |
4,410 |
4,900 |
0,110 |
0,020 |
0,090 |
0,90000 |
0,405 |
66,9 |
656,289 |
4,300 |
4,865 |
0,000 |
-0,015 |
0,015 |
0,15000 |
0,011 |
Tab.3 Tabela pomiarów ugięć w środku przęsła i przemieszczenia podpór. Waga = 66,9 kG
Odczyt z czujników |
Wartości rzeczywiste [cm] |
|
|
|
||||||
obciążenie |
ugięcie |
przem. podpór |
podpora |
ugięcie |
podpora |
|
|
|
||
kG |
kN |
czujnik 2 |
czujnik1 |
czujnik 3 |
δ 1 |
δ 2 |
δ 3 |
y`[cm] |
ymax |
P/ymax[kN/m] |
66,9 |
0,669 |
10,000 |
7,000 |
4,000 |
0,000 |
0,000 |
0,000 |
0,0000 |
0,0000 |
- |
116,9 |
1,169 |
10,430 |
7,000 |
3,985 |
0,000 |
0,430 |
-0,015 |
0,4225 |
0,4225 |
276,665436 |
166,9 |
1,669 |
10,860 |
7,010 |
3,965 |
0,010 |
0,860 |
-0,035 |
0,8375 |
0,8376 |
199,266451 |
216,9 |
2,169 |
11,300 |
7,015 |
3,945 |
0,015 |
1,300 |
-0,055 |
1,2650 |
1,2652 |
171,429655 |
266,9 |
2,669 |
11,740 |
7,020 |
3,930 |
0,020 |
1,740 |
-0,070 |
1,6950 |
1,6955 |
157,419929 |
298,9 |
2,989 |
12,025 |
7,025 |
3,920 |
0,025 |
2,025 |
-0,080 |
1,9725 |
1,9733 |
151,475185 |
266,9 |
2,669 |
11,750 |
7,025 |
3,920 |
0,025 |
1,750 |
-0,080 |
1,6975 |
1,6981 |
157,177703 |
216,9 |
2,169 |
11,320 |
7,020 |
3,935 |
0,020 |
1,320 |
-0,065 |
1,2775 |
1,2779 |
169,734496 |
166,9 |
1,669 |
10,890 |
7,015 |
3,950 |
0,015 |
0,890 |
-0,050 |
0,8575 |
0,8576 |
194,602775 |
116,9 |
1,169 |
10,460 |
7,010 |
3,980 |
0,010 |
0,460 |
-0,020 |
0,4450 |
0,4450 |
262,672723 |
66,9 |
0,669 |
10,020 |
7,000 |
4,035 |
0,000 |
0,020 |
0,035 |
0,0375 |
0,0375 |
- |
P/ymax = 193,382706 |
||||||||||
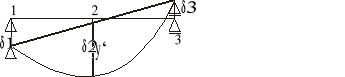
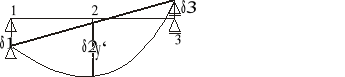
Schemat ugięcia belki:
Ugięcie przy uwzględnieniu osiadania podpór: ![]()
![]()
Ugięcie całkowite po uwzględnieniu zwichrzenia: ![]()
Wykres zależności siły od ugięcia:
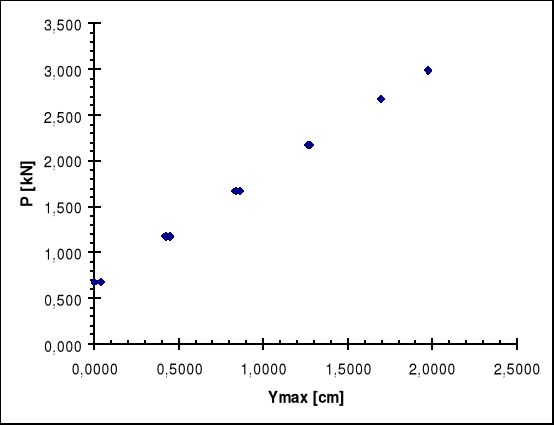
![]()
![]()
Moduł Younga: ![]()
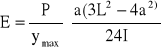
![]()
![]()
E = 289,22 MPa
Wnioski.
Wynik uzyskanego modułu Younga
Rzeczywista praca belki jest zbliżona do założeń.
Poprawka na zwichrzenie ma znikomy wpływ na ugięcie, większy ma osiadanie podpór.
Wyszukiwarka
Podobne podstrony:
Metale Laboratorium, Spr-metale, Politechnika Wrocławska
sprawko moo1, Automatyka i Robotyka, Semestr III, Metody Obliczeniowe Optymalizacji, Gotowce, labki
Metale Laboratorium, Konspekt, Ćwiczenie laboratoryjne nr 1 z Konstrukcji Metalowych
Metale Laboratorium, Laborki z Metali, Politechnika Wrocławska
Metale Laboratorium, bart, 1
Metale Laboratorium, KRZYZ
CHEMIA LABORATORIUM SPRAWOZDANIE Działanie podstawowych zasad i kwasów na metale wersja 2
Urządzenia peryferyjne lab1, Studia, PWR, 5 semestr, Urządzenia peryferyjne, laboratorium
poziomy energetyczne konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laborato
M gr lab1 okładka, PWR, PWR, 4 semestr, Grunty, Laboratorium
Kopia LABORATORIUM-nasze, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1
LABORATORIUM, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1), Sprawozda
Laboratorium, plsql lab1, 1
LABORATORIUM-nasze v2, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1),
przerwa energetyczna konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laborato
Sprawozdanie10, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
ole lab1, Energetyka AGH, V semestr, Automatyka, laboratoria
10-LAB, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki
więcej podobnych podstron