Systemy sterowania
Obiektowo zorientowana reprezentacja systemów
W MATLABie do opisu systemów zastosowano mechanizmy obiektowe. Oznacza to, że opis systemu jest reprezentowany przez nazwę obiektu, z którym związane są pola danych, które można określić jako własności obiektu i operacje, które na tych danych można wykonywać, które nazywamy metodami. Dzięki zastosowaniu mechanizmów obiektowych uproszczono składnię i zmniejszono liczbę funkcji. Możliwe jest tworzenie obiektów systemowych dla trzech różnych form opisu
transmitancji systemu
zer, biegunów, wzmocnienia
równań stanu.
Można budować systemy typu zarówno SISO jak i MIMO, ciągłe i dyskretne.
Tworzenie obiektów systemowych
Opis w postaci transmitancji (tf)
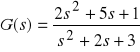
num = [2 5 1];
den = [1 2 3];
sys1 = tf(num, den)
Współczynniki wielomianów licznika i mianownika funkcji transmitancji podajemy w kolejności malejącej.
Argumenty macierzowe można podać bezpośrednio w wywołaniu funkcji tf
![]()
sys2 = tf(1,[1 1])
W systemach MIMO opis ma postać macierzy transmitancji![]()
,gdzie l jest liczbą wyjść obiektu, a s liczbą jego wejść,![]()
jest transmitancją między j-tym wejściem, a i-tym wyjściem obiektu. Argumenty funkcji tf mają postać zbiorów macierzy liczników i mianowników elementów macierzy transmitancji.
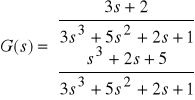
N = {[3 1];[1 0 2 5]}
D = {[3 5 2 1];[3 5 2 1]}
sys3 = tf(N,D)
tak jak i poprzednio argumenty funkcji można wpisać bezpośrednio w wywołaniu funkcji
sys3 = tf({[3 1];[1 0 2 5]},{[3 5 2 1];[3 5 2 1]})
W ogólnym przypadku N(i,j) jest wektorem wierszowym zawierającym współczynniki wielomianu licznika![]()
, a D(i,j) jest wektorem wierszowym współczynników mianownika ![]()
.
b) Opis w formie zera bieguny wzmocnienie (zpk)
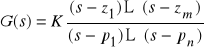
K - wielkość skalarna (wzmocnienie), ![]()
- zera funkcji transmitancji, ![]()
- bieguny. Zera i/lub bieguny mogą być wielkościami zespolonymi.
Systemy SISO tworzymy za pomocą funkcji zpk, podając jako argumenty wektory zer, biegunów i wzmocnienie. Np. wywołanie
sys1=zpk(0,[1-i, 1+i, 2],-2)
odpowiada transmitancji
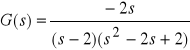
Jeśli brak zera, jako argument podajemy macierz pustą []
sys2 = zpk([],-1,1)
odpowiada transmitancji
![]()
Systemy MIMO wymagają podania funkcji zpk zbiorów macierzy zer, biegunów i macierz wzmocnień.
sys = zpk(Z,P,K)
Z - zbiór macierzy zer rozmiaru lxs, (Z{i,j} zawiera wektor wierszowy zer transmitancji ![]()
P - zbiór macierzy biegunów rozmiaru lxs, (P{i,j} zawiera wektor wierszowy biegunów transmitancji ![]()
.
K - macierz wzmocnień rozmiaru lxs (K(i,j) zawiera wzmocnienie transmitancji ![]()
.
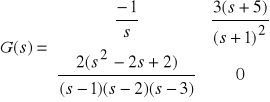
Z = {[],-5;[1-i, 1+i],[]}
P = {0,[-1, -1];[1, 2, 3], []}
K = [-1, 3;2, 0]
sys3 = zpk(Z,P,K)
Opis w postaci równań stanu (ss)
Macierzowy postać równań stanu
![]()
sys = ss(A,B,C,D)
Na przykład dla opisu
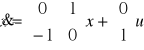
![]()
sys = ss([0, 1;-1, 0],[0; 1],[1, 0], 0)
Systemy 2. rzędu
ord2 - generuje opis ciągłego systemu SISO 2. rzędu przy danej pulsacji własnej![]()
i współczynniku tłumienia ![]()
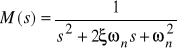
Można utworzyć macierze opisu stanowego:
[A, B, C, D] = ord2(wn, z)
(wn - pulsacja własna, z - współczynnik tłumienia) lub współczynniki wielomianów licznika i mianownika funkcji transmitancji.
[licz, mian] = ord2(wn, z)
Znajdziemy odpowiedź na wymuszenie skokiem jednostkowym systemu z jednostkowym sprzężeniem zwrotnym, którego transmitancja przy otwartej pętli sprzężenia zwrotnego ma postać:
![]()
[licz, mian] = ord2(1,0.2);
sys = tf(licz, mian)
step(sys)
Odzyskiwanie danych o systemie na podstawie obiektu
Po utworzeniu systemu za pomocą funkcji opisanych wcześniej, możemy z powrotem odzyskać macierze odpowiednich współczynników systemu.
Dla obiektu sys reprezentującego transmitancję po wywołaniu
[num, den, Ts] = tfdata(sys)
MATLAB utworzy zbiory macierzy num , den ze współczynnikami wielomianów odpowiednio liczników i mianowników. Ts jest okresem próbkowania. Dla systemów ciągłych jest on zawsze równy 0. Wartość Ts = -1 oznacza, niezdefiniowany okres próbkowania. Wielkość Ts jest istotna dla systemów dyskretnych. Podobnie możemy uzyskiwać dane o systemach opisanych przez zera-bieguny-wzmocnienie
[z, p, k, Ts] = zpkdata( sys )
Zauważmy, że zarówno num, den jak i z, p i k są zbiorami macierzy (nawet dla systemu SISO)
Dla równań stanu mamy
[a, b, c, d, Ts] = ssdata(sys)
a, b, c, d są macierzami w opisie stanu systemu.
Podstawowe funkcje do analizy systemów
pole - wyznaczanie biegunów funkcji transmitancji
p = pole(sys)
Jeśli sys jest stanowym opisem systemu, to funkcja zwraca wartości własne macierzy A.
tzero - zera funkcji transmitancji
z = tzero(sys)
[z, k] = tzero(sys)
Po wywołaniu funkcji, z zawiera wektor zer, a k wzmocnienie (w zapisie zera-bieguny-wzmocnienie)
pzmap - graficzne przedstawienie zer i biegunów funkcji transmitancji na płaszczyźnie zespolonej s. Zera są reprezentowane przez `o', a bieguny przez `x'.
pzmap(sys)
[p, z] = pzmap(sys)
Drugi sposób wywołania umieszcza w p bieguny, a w z zera funkcji transmitancji. Wykres zer i biegunów nie jest wówczas rysowany.
damp - wyznacza bieguny oraz odpowiadające im współczynniki tłumienia i pulsacje własne systemu.
[wn, z] = damp(sys)
[wn, z, p] = damp(sys)
Po wywołaniu wektor wn zawiera pulsacje własne![]()
,wektor z zawiera współczynniki tłumienia![]()
. Drugie wywołanie umieszcza w wektorze p bieguny systemu.
step - wyznaczenie odpowiedzi skokowej na pobudzenie jednostkowe przy zerowych warunkach początkowych.
step(sys)
step(sys, t)
Drugie wywołanie szkicuje wykres w zadanym czasie, np. t=0:dt:Tf.
Można szkicować odpowiedzi wielu systemów na jednym wykresie:
step(sys1, ..., sysN)
step(sys1, ..., sysN,t)
Można stosować różne style i kolory linii:
step(sys1,'PlotStyle1', ..., sysN, `PlotStyleN')
Jeśli użyjemy jednego z wywołań
y = step(sys, t)
[y, t] = step(sys)
[y, t, x] = step(sys) % tylko dla opisu w formie równań stanu
to odpowiedzi zostaną wyznaczone i umieszczone w wektorze y bez szkicowania wykresów. Dla opisu stanowego wektor x przyjmie wartości stanu w momentach czasu określonych przez t.
impulse - odpowiedź impulsowa systemu przy zerowych warunkach początkowych. Dla systemów ciągłych jest to odpowiedź na pobudzenie deltą Diraca![]()
. Składnia wywołania jest identyczna jak dla funkcji step.
lsim - wyznaczenie odpowiedzi czasowej systemu na dowolne pobudzenie.
lsim(sys, u, t)
wykreśla odpowiedź na pobudzenie, którego próbki zawiera wektor u, a odpowiadający mu czas wektor t. Próbki czasu powinny mieć równe odstępy, a więc t=0:dt:Tf. Wymiary u i t powinny być zgodne.
lsim(sys, u, t, x0)
lsim(sys1, ..., sysN, u, t)
lsim(sys1, ..., sysN, u, t, x0)
lsim(sys1, `PlotStyle1', ..., sysN, `PlotStyleN', u, t)
[y, t, x] = lsim(sys, u, t, x0)
rlocus - metoda miejsc geometrycznych. Metoda graficzna pozwalająca na wyznaczenie lokalizacji pierwiastków równania charakterystycznego systemu SISO na płaszczyźnie zespolonej s w zależności od pewnego parametru tego równania. Jeśli transmitancja otwartej pętli systemu ma postać ![]()
, gdzie K jest pewnym parametrem, to równanie charakterystyczne systemu z zamkniętą pętlą ujemnego sprzężenia zwrotnego ma postać ![]()
. Jest oczywiste, że położenie biegunów jest uzależnione od wartości K i ma ono z kolei pośredni wpływ na kształt charakterystyk czasowych i częstotliwościowych systemu. Przedstawienie graficzne linii pierwiastkowych wymaga znajomości transmitancji pętli systemu.
Przedstawimy linie pierwiastkowe dla systemu na rysunku poniżej
Transmitancja pętli jest równa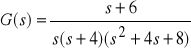
.
num = [1 6]; % licznik transmitancji
den = conv([1 4 0],[1 4 8]); %mianownik transmitancji
sys = tf(num, den) % transmitancja systemu
rlocus( tf); %wykreślenie linii pierwiastkowych
Poszczególne kolory odpowiadają różnym biegunom równania charakterystycznego
Funkcję rlocus można wywołać dla konkretnych wartości K,
K = 0:0.5:10;
rlocus(sys,K)
Przy wywołaniu
[r, K] = rlocus(sys)
r = rlocus(sys, K)
zwracany jest wektor z kolejnymi wartościami zespolonymi trajektorii biegunów oraz odpowiadający im wektor wzmocnień K. Wykres linii pierwiastkowych nie jest rysowany. Na rysunkach poniżej podano przykładowe konfiguracje systemu i sposób wyznaczenia transmitancji systemu.
sgrid - dorysowanie siatki na wykresie zer i biegunów (patrz pzmap) lub linii pierwiastkowych (rlocus)
rlocus(sys)
sgrid
rlocfind - znajdowanie wartości wzmocnienia K odpowiadającej wybranej lokalizacji biegunów równania charakterystycznego ciągłego lub dyskretnego systemu SISO. Przed wywołaniem tej funkcji aktywnym oknem graficznym powinno być okno z rysunkiem linii pierwiastkowych.
Analiza systemów w dziedzinie częstotliwości
bode - wyznaczenie logarytmicznych charakterystyk amplitudowo-fazowych systemu. Dla systemu opisanego transmitancją
![]()
następujące komendy szkicują wykresy Bodego
sys = zpk(-10, [0, -2, -5], 10);
bode(sys)
Zakres pulsacji odpowiadający osi odciętych jest dobierany automatycznie na podstawie zer i biegunów systemu. Można jednak wymusić szkicowanie wykresów w zadanym przedziale pulsacji
bode(sys, w)
gdzie w = {wmin, wmax} określa zakres pulsacji![]()
, którą podajemy w rad/s.
w = {0.1, 1000}
bode( sys, w)
Możliwe jest (np. w celu porównania) szkicowanie wielu charakterystyk na jednym rysunku
bode(sys1, sys2,...,sysN)
bode(sys1, sys2,...,sysN, w)
Wykresy mogą być rysowane różnymi stylami
bode(sys1, `PlotStyle1',...,sysN, `PlotStyleN')
Porównajmy charakterystyki dwóch systemów:
![]()
![]()
![]()
sys1=tf(8, [1 6 12 8])
sys2=tf(2.31, [1, 2.936, 2.31]
bode(sys1, `r--`,sys2,'gx')
Wywołania z argumentami lewostronnymi dają wartości modułu i argumentu w podanym zakresie częstotliwości, lecz nie szkicują wykresu
[mag, phase, w] = bode(sys)
[mag, phase] = bode(sys)
mag - wzmocnienie, phase - faza w stopniach, w - zakres ![]()
w rad/s. Zamiana wzmocnienia na wartości w decybelach jest wykonywana komendą
magdb=20*log10(mag)
mag i phase - trójwymiarowe tablice o wymiarach
(liczba wyjść)x(liczba wejść)x(długość wektora w)
Dla systemów SISO, mag(1, 1, k) i phase(1, 1, k) są odpowiednio wartością wzmocnienia i fazy dla ![]()
. Systemy typu MIMO ![]()
oraz ![]()
, gdzie ![]()
jest transmitancją widmową systemu obliczoną dla pulsacji ![]()
.
Tworzenie systemów złożonych
append - grupowanie wejść i wyjść podsystemów
sys = append(sys1, ..., sysN)
Tworzenie modelu złożonego przedstawiono na rysunku
Jeśli systemy składowe mają funkcje transmitancji równe![]()
,…,![]()
, to wypadkowa macierz transmitancji jest blokowo diagonalna

.
Dla modeli stanowych sys1 i sys2 opisanych macierzami![]()
i ![]()
wypadkowy model stanu wygląda następująco
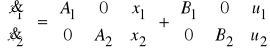
,
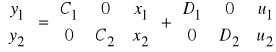
.
parallel - połączenie równoległe systemów. Wynik działania funkcji wyjaśnia rysunek.
sys = parallel(sys1, sys2)
Taki sam efekt można uzyskać pisząc
sys = sys1 + sys2
Możliwe jest tworzenie ogólniejszych połączeń równoległych za pomocą wywołania
sys = parallel(sys1, sys2, inp1, inp2, out1, out2)
Parametry inp1 i inp2 są wektorami numerów wejść systemów odpowiednio sys1 i sys2, które mają być połączone równolegle i traktowane jako wejścia wspólne systemu złożonego. Wejścia te oznaczono jako![]()
i![]()
dla systemów odpowiednio sys1 i sys2. Analogicznie, parametry out1 i out2 są wektorami numerów wyjść systemów sys1 i sys2, które będą zsumowane. Sytuacja taka jest przedstawiona na rysunku.
series - połączenie szeregowe systemów. Wynik działania funkcji przedstawiono na rysunku.
sys = series(sys1, sys2)
Zamiast powyższej konstrukcji można zastosować operator mnożenia.
sys = sys1*sys2
Powyższe konstrukcje są równoważne.
Można tworzyć ogólniejsze połączenia przez wskazanie wyjść systemu sys1 i wejść systemu sys2, które mają być połączone. Składnia wywołania jest następująca:
sys = series(sys1, sys2, out1, in2)
out1 jest wektorem wyjść systemu sys1, a in2 wektorem wejść systemu sys2, które mają być połączone. Wywołanie komendy tworzy system przedstawiony na rysunku.
Wypadkowy system ma wejście u i wyjście y.
feedback - utworzenie systemu ze sprzężeniem zwrotnym. Wywołanie funkcji
sys = feedback(sys1, sys2)
tworzy system z ujemnym sprzężeniem zwrotnym, w którym w gałęzi sprzężenia zwrotnego znajduje się blok sys2. Rezultat przedstawiono na rysunku:
Znak sumowania w pętli można zmieniać podając dodatkowy argument. Komenda
sys = feedback(sys1, sys2, +1)
utworzy system o dodatnim sprzężeniu. W sytuacji, gdy parametr znaku jest pominięty, przyjmowane jest domyślnie ujemne sprzężenie zwrotne.
Ogólniej można tworzyć systemy ze sprzężeniem zwrotnym przy pomocy wywołań
sys = feedback(sys1, sys2, fin, fout)
sys = feedback(sys1, sys2, fin, fout, sign)
Zostanie wówczas utworzony system przedstawiony na rysunku. Wektor fin zawiera numery tych wejść systemu sys1, które są częścią pętli sprzężenia, natomiast fout zawiera numery wjść sys1, które biorą udział w pętli. Parametr sign reprezentuje znak sprzężenia. Domyślnie przyjęto znak ujemny. By utworzyć dodatnią pętlę piszemy
sys = feedback(sys1, sys2, fin, fout, +1)
Obiekty statyczne można podawać jako zwykłe macierze
sys = feedback(sys1, 2)
jednak co najmniej jeden z łączonych podsystemów powinien być obiektem. Jeśli np. łączymy dwa wzmacniacze o wzmocnieniach K1 i K2, to należy to zrobić następująco:
sys = feedback(tf(K1), K2)
Słownik ważniejszych pojęć
SISO (Single Input Single Output) - system o jednym wejściu i jednym wyjściu (system skalarny).
MIMO (Multiple Input Multiple Output) - systemy o wielu wejściach i wyjściach (systemy wielowymiarowe).
Charakterystyka czasowa - graficzne lub analityczne przedstawienie przebiegu czasowego odpowiedzi układu na określony sygnał wejściowy. Podstawowymi charakterystykami czasowymi dla układów liniowych są: odpowiedź impulsowa oraz odpowiedź na skok jednostkowy. Znajomość charakterystyk czasowych układu umożliwia ocenę jakości sterowania na podstawie odczytanych z wykresu wskaźników (np. przeregulowania, czasów narastania i regulacji).
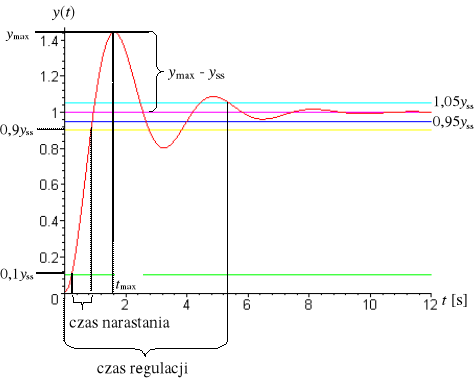
Czas narastania - czas, który upływa od chwili zmiany sygnału wyjściowego układu o określonej wartości początkowej, wywołanej skokiem jednostkowym sygnału wejściowego do chwili, w której osiągnie on określoną część swej wartości ustalonej![]()
. Praktycznie przyjmuje się, że jest to czas potrzebny do wzrostu amplitudy sygnału od 0,1 do 0,9 wartości ustalonej. W przypadku układu liniowego czas narastania nie zależy od wartości ustalonej. Jest on miarą inercyjności (wskaźnikiem szybkości odpowiedzi) układu i zależy od jego stałych czasowych.
Czas regulacji - czas, po upływie którego uchyb przejściowy wielkości regulowanej jest stale mniejszy od dopuszczalnego uchybu ustalonego.
Przeregulowanie - maksymalny uchyb wielkości regulowanej![]()
od jej wartości ustalonej![]()
wyrażony w jednostkach względnych:
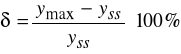
.
Najczęściej rozpatruje się przeregulowanie w układach stabilnych analizując odpowiedź układu na wymuszenie skokowe.
Uchyb regulacji - różnica między wartością zadaną wielkości regulowanej a jej wartością rzeczywistą:![]()
. Uchyb regulacji jest sumą dwóch składowych: ![]()
, gdzie![]()
nazywa się uchybem w stanie ustalonym, a ![]()
- uchybem przejściowym., istniejącym w stanie nieustalonym. Uchyb regulacji jest sygnałem wejściowym regulatora. Wartość graniczną![]()
nazywa się uchybem statycznym lub ustalonym. Wielkość ta stanowi miarę dokładności statycznej układu.
Dekada - dla zmiennej niezależnej ω dekada jest długością przedziału [ω, 10ω], bowiem ![]()
.
Oktawa - dla zmiennej niezależnej ω oktawa jest długością przedziału [ω, 2ω]. Mamy ![]()
, wobec tego 1 oktawa ≈ 0,3 dekady.
Decybel (dB) - jeśli dwie wielkości (np. rzędne na wykresie Bodego)![]()
i![]()
różnią się o 1 decybel to znaczy, że ![]()
. Zatem ![]()
lub ![]()
. Bel (B) jest jednostką większą równą 10 decybelom, tzn. 1 B = 10 dB.
Charakterystyka amplitudowo fazowa - w ogólnym przypadku![]()
jest funkcją zespoloną zmiennej rzeczywistej ω, której moduł A(ω) jest nazywany charakterystyką amplitudową, a argument φ(ω) jest nazywany charakterystyką fazową. Logarytm ![]()
jest również funkcją zespoloną o składowej rzeczywistej ![]()
i składowej urojonej ![]()
.
Wykresy Bodego charakterystyki amplitudowo fazowej są to a) wykres ![]()
w funkcji logarytmu dziesiętnego pulsacji ω, b) wykres fazy ![]()
w funkcji logarytmu dziesiętnego pulsacji ω. Na wykresach tych jednostką osi odciętych![]()
jest dekada. Jednostką osi rzędnych![]()
charakterystyki amplitudowej jest decybel, a jednostką osi rzędnych charakterystyki fazowej![]()
jest stopień.
Transmitancja minimalnofazowa - transmitancja, której wszystkie zera i bieguny znajdują się w lewej półpłaszczyźnie zmiennej zespolonej s. Układy minimalnofazowe charakteryzują się tym, że na podstawie charakterystyki amplitudowej możemy w sposób jednoznaczny wyznaczyć ich charakterystykę fazową i na odwrót, przy danej charakterystyce fazowej można jednoznacznie wyznaczyć charakterystykę amplitudową. Własności tej nie posiadają układy nieminimalnofazowe.
Transmitancja nieminimalnofazowa - transmitancja, która posiada bieguny i/lub zera zlokalizowane w prawej półpłaszczyźnie.
Stabilność względna systemu jest określona przez parametry takie jak zapas wzmocnienia i zapas fazy, które pozwalają na określenie „jak daleko” system znajduje się od granicy stabilności wyznaczonej przez punkt (-1, j0). Parametry te wyznaczamy na ogół metodą graficzną na podstawie wykresów Bodego lub Nyquista układów o minimalnofazowej transmitancji pętli. Transmitancję pętli wyraża się iloczynem transmitancji gałęzi głównej![]()
i transmitancji gałęzi sprzężenia zwrotnego![]()
.
Zapas wzmocnienia w decybelach wyrażamy zależnością
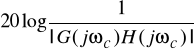
.
W celu jego obliczenia trzeba wyznaczyć pulsację![]()
, przy której wykres Nyquista przecina lewą półoś rzeczywistą (patrz rysunek), co zachodzi przy warunku
![]()
.
Zapas fazy w stopniach określamy jako kąt, o który należy obrócić wykres Nyquista transmitancji ![]()
tak by punkt jego przecięcia z okręgiem jednostkowym pokrył się z punktem (-1, j0); patrz rysunek. Wyrażamy go wzorem
![]()
![]()
.
W celu jego obliczenia należy wyznaczyć pulsację![]()
, dla której wykres Nyquista przecina okrąg jednostkowy, co zachodzi przy warunku
![]()
.
Wykres Nyquista charakterystyki amplitudowo fazowej we współrzędnych kartezjańskich ![]()
, ![]()
, gdy ω zmienia się od 0 do ∞. Równoważnie można ten wykres definiować we współrzędnych biegunowych![]()
),![]()
.
Wykres Nicholsa charakterystyki amplitudowo fazowej nazywamy wykres Nyquista jej logarytmu, tzn. zbiór wszystkich wartości funkcji![]()
na płaszczyźnie zespolonej przy ω zmieniającym się od 0 do ∞. Jednostką osi rzędnych jest dB, a odciętych stopień.
Szczyt rezonansowy Mp maksymalna wartość modułu charakterystyki amplitudowej ![]()
.
Pulsacja rezonansowa ωp - pulsacja, przy której występuje szczyt rezonansowy![]()
Linearyzacja - zastąpienie układu równań różniczkowych nieliniowych układem równań różniczkowych liniowych, w celu uproszczenia lub umożliwienia analizy. Polega ona na rozkładzie funkcji nieliniowych w szereg potęgowy i uwzględnieniu tylko liniowych członów rozkładu.
Szerokość pasma BW - przedział pulsacji od 0 do![]()
, przy której następuje spadek wartości charakterystyki amplitudowej ![]()
o 3 dB w stosunku do wartości tejże charakterystyki dla ![]()
.
Równanie charakterystyczne - równanie uzyskane przez przyrównanie do zera wielomianu w mianowniku funkcji transmitancji systemu z zamkniętą pętlą sprzężenia zwrotnego.
Jacek Cichosz
y
r
e
G
K
-
sys = G
sys=GH
-
K
G
H
F
sys=FG
-
K
G
sys1
sys1
.
.
.
![]()
![]()
![]()
![]()
sys1
sys2
u
y
sys
sys
y
u
sys2
sys1
v1
v2
z1
u1
z2
u2
y1
y2
sys1
sys2
u
y
sys
sys
y
u
sys2
sys1
v2
z1
y1
u2
sys1
sys2
u
y
-
y
u
sys2
sys1
-
z
v
ω→∝
ω→0
ω=ωg
Zapas
fazy
1
-1
0
Re(GH)
jIm(GH)
jIm(GH)
Re(GH)
0
-1
|G(jωc)H(jωc)|
ω=ωc
ω→0
ω→∝
Wyszukiwarka
Podobne podstrony:
Matlab-kurs, Modele systemow ciaglych, Symulacja:
Kurs systemu zarządzania treścią Joomla! Część siódma moduły
Matlab-kurs, MATLAB, MATLAB
kurs matlaba, Lab4 KURS MATLABa, KURS MATLABa
kolokwium rok II 20070117, Prywatne, 1 SUM, infa, Matlab kurs pl (bd4ty3), matlab
Matlab kurs SIMULINK
Wyciąg z poleceń MATLABA, kurs Matlaba PL
Matlab kurs
J Kossecki, Cele i metody badania przeszłości w różnych systemach sterowania społecznego
System i metody sterowania w logistyce
KOMPUTEROWE SYSTEMY STEROWANIA Nieznany
mikroprocesorowy system sterowania skladem mieszanki silnika zasilanego gazem plynnym typ al700
Opracowanie pytań na egzamin z Systemów Sterowania Maszyn i Robotów u Salamandry
Żołnierka, teoria systemów, METODY OPISU CIĄGŁYCH LINIOWYCH JEDNOMIAROWYCH OBIEKTÓW STEROWANIA (2)
Labolatorium projektowania układów i systemów sterowania, Narzędzia komputerowego wspomagania projek
Czasy miedzyzielone III-I, Studia Mgr, II semestr mgr, System sterowania ruchem
Labolatorium komputerowych systemów automatyki, Systemy wizualizacji i sterowania, Politechnika Lube
więcej podobnych podstron